Cho tam giác ABC vuông tại A ,từ trung điểm E của Ac vẽ EF vuông góc với BC.
a. Chứng minh AF=BE.CosC
b. Cho BC=20, SinC = 0,6. Tính diện tích tứ giác AEFB
tam giác ABC vuông tại A. Từ trung điểm E của AC vẽ EF vuông góc với BC.
a, C/m: AF=BE.cosC
b, BC =20, sin C=0,6. Tinh SAEFB
Cho tam giác ABC vuông tại A.Từ trung điểm E của cạnh AC,vẽ EF vuông góc với BC
a,Chứng minh AF=BE.Cos C
b, cho BC =20cm, sinC =0,6Tính diện tích AEFB
Cho tam giác ABC vuông tại A. Từ trung điểm E của cạnh AC kẻ EF vuông góc với BC tại F.
a) Cho BC = 20cm, sinC = 0,6. Giải tam giác ABC;
b) Chứng minh rằng: AC2 = 2CF.CB
c) Chứng minh: AF = BE.cosC
Cho tam giác ABC vuông tại A. Từ trung điểm E của cạnh AC, kẻ EF vuông góc với BC tại F
a) Cho BC = 20 cm và sinC = 0,6. Giải tam giác ABC
b) Chứng minh AC2 = \(2CF\times CB\)
c) Chứng minh AF = BC ✖ cosC
b: Xét ΔCFE vuông tại F và ΔCAB vuông tại A có
\(\widehat{C}\)chung
Do đó: ΔCFE\(\sim\)ΔCAB
Suy ra: \(\dfrac{CF}{CA}=\dfrac{CE}{CB}\)
\(\Leftrightarrow CF\cdot CB=CE\cdot CA\)
\(\Leftrightarrow CF\cdot CB=CA\cdot\dfrac{1}{2}AC\)
\(\Leftrightarrow AC^2=2\cdot CF\cdot CB\)
Cho tam giác ABC vuông tại A . Từ trung điểm E của cạnh AC kẻ EF vuông góc với AC tại F
a) Cho BC = 20cm, sinC = 0,6. Giải tam giác ABC;
b) Chứng minh rằng : AC2 = 2CF.CB
c) Chứng minh : AF = BC.cosC
1. Cho tam giác ABC vuông tại A, đường cao AH. Từ trung điểm E của AC vẽ EF vuông góc với BC tại F. Chứng minh:
a) EF2=\(\dfrac{BH.CH}{4}\)
b) AF=BE.cosC
a) Xét \(\Delta CAH:\) ta có: E là trung điểm AC và \(EF\parallel AH(\bot BC)\)
\(\Rightarrow F\) là trung điểm CH \(\Rightarrow EF\) là đường trung bình \(\Rightarrow EF=\dfrac{1}{2}AH\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=BH.CH\)
Ta có: \(EF^2=\left(\dfrac{1}{2}AH\right)^2=\dfrac{1}{4}AH^2=\dfrac{1}{4}.BH.HC\)
b) Ta có: \(\angle BAE+\angle BFE=90+90=180\Rightarrow ABFE\) nội tiếp
\(\Rightarrow\angle FBE=\angle FAE\)
Xét \(\Delta CBE\) và \(\Delta CAF:\) Ta có: \(\left\{{}\begin{matrix}\angle CBE=\angle CAF\\\angle BCAchung\end{matrix}\right.\)
\(\Rightarrow\Delta CBE\sim\Delta CAF\left(g-g\right)\Rightarrow\dfrac{AF}{BE}=\dfrac{AC}{BC}=cosC\Rightarrow AF=cosC.BE\)
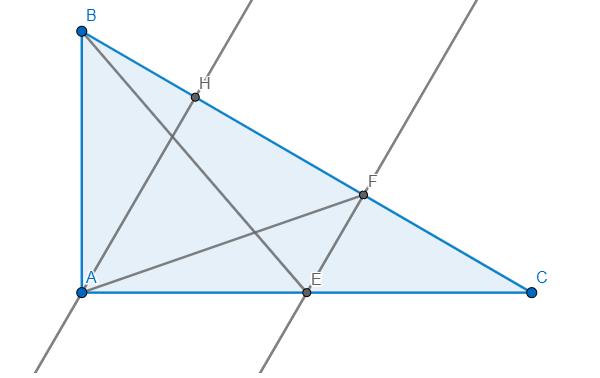
tam giác ABC vuông tại A , đường cao AH. từ trung điểm E của AC vẽ EF vuông góc với BC tại F
chứng minh AF=BE.cosC
Cho tam giác ABC vuông tại A. Từ trung điểm E của AC kẻ EF vuông góc BC.
a) CM: AF = BE. cos C
b) AF giao BE tại O. Biết BC = 10 cm, sin C = 0,6. Tính diện tích tứ giác ABFE và sin AOB.
mk chỉ dải tóm tắt thôi có gì ko hiểu bạn nhắn tin cho mk cùng
https://olm.vn/hoi-dap/detail/189938041517.html
ý 2 phần b mk cũng chưa làm đc
a, ta có Cos C=\(\frac{CF}{EC}\)
C/m tam giác CEF đồng dạng với tam giác CBA (g-g)
=> \(\frac{CF}{EC}=\frac{AC}{BC}\)
=> tam giác AFC và tam giác BEC dồng dạng (c-g-c)
=>\(\frac{CF}{EC}=\frac{AF}{AE}\)
=> Cos C =\(\frac{AF}{BE}\)=> BE.Cos C= BE.\(\frac{AF}{BE}\)=AF(đpcm)
b,
bn áp dụng các hệ thức về góc và cạnh trong tam giác vuông
mỗi cạnh góc vuông bằng cạnh huyền.Sin góc đối để tính AB,AC trong tam giác ABC vuông
=> AE=EC=AC:2=...(bn tu tinh nha)
xét tam giác CEF vuông tại C
lại áp dụng công thức trên để tính È
=> FC=....(Theo Pi-ta-go)
=>BF=BC-FC
=>BF=....
=>bn tính SABE VÀ SBEF sau đó cộng lại là ra SABFE
NẾU CÓ BN NÀO GIẢI ĐƯỢC CÂU B PHẦN 2 THÌ GIÚP MK VS*****CHÚC BẠN HỌC GIỎI*****Giúp mình với mình cần gấp :))
Cho tam giác vuông ABC ( tại A ). Gọi E là trung điểm của AC. Hạ È vuông góc với BC.
CMR : a, AF = BE.CosC
b, Biết BC = 10cm, SInC = 0,6. Tính diện tích ABFE
c, Gọi À giao với BE tại O.Tính SinAOB ?
b, sinC = AB/BC=EF/EC =0,6 -> AB=6 ->AC=8 -> AE=EC=4
-> Sabe = 1/2. AB.AE=12. tt: Sbef=1/2.BF.EF= 8,16-> Sabef= 20,16