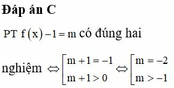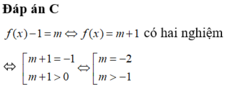Tìm tất cả giá trị thực của tham số m để phương trìn f (x) -1=m có đúng 2 nghiệm

Những câu hỏi liên quan
Cho hàm số
y
f
x
có đồ thị như hình vẽ . Tìm tất cả các giá trị thực của tham số m để phương trình
f
x
−
m
0
có đúng 2 nghiệm và giá trị tuyệt đối của 2 nghiệm này đều lớn hơn 1 A.
m
−
4
B.
−
4
m
−
3
C.
m...
Đọc tiếp
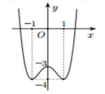
Cho hàm số y = f x có đồ thị như hình vẽ . Tìm tất cả các giá trị thực của tham số m để phương trình f x − m = 0 có đúng 2 nghiệm và giá trị tuyệt đối của 2 nghiệm này đều lớn hơn 1
A. m > − 4
B. − 4 < m < − 3
C. m > − 3
D. − 4 < m ≤ − 3
Đáp án C
Khi m > -3 thì phương trình f(x) = m có hai nghiệm lớn hơn 1. Do đó chọn phương án C.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định, liên tục trên R và có bảng biến thiên như sau:Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-1m có đúng 2 nghiệm A. -2 m -1 B. m 0, m -1 C. m -2, m -1 D. m -2, m ≥ -1
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như sau:

Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-1=m có đúng 2 nghiệm
A. -2 < m < -1
B. m > 0, m = -1
C. m = -2, m > -1
D. m = -2, m ≥ -1
Chọn đáp án C
Phương pháp
Số nghiệm của phương trình f(x)=m là số giao điểm của đồ thị hàm số y=f(x) và y=m song song với trục hoành.
Cách giải
Ta có:
![]()
Số nghiệm của phương trình f(x)=m là số giao điểm của đồ thị hàm số y=f(x) và y=m+1 song song với trục hoành.
Từ BBT ta thấy để phương trình f(x)-1=m có đúng 2 nghiệm thì
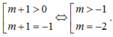
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định, liên tục trên
ℝ
và có bảng biến thiên như sau: Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-1m có đúng 2 nghiệm. A. -2m-1 B. m0,m-1 C. m-2,m-1 D. m-2,m
≥
-1
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên ℝ và có bảng biến thiên như sau:
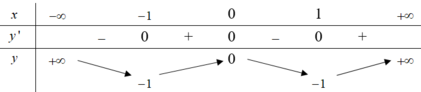
Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-1=m có đúng 2 nghiệm.
A. -2<m<-1
B. m>0,m=-1
C. m=-2,m>-1
D. m=-2,m ≥ -1
Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x - 2018) - 2| = m có đúng 3 nghiệm
3: cho hàm số f(x)=ax^2+bx+c có tọa độ đỉnh (2;-1) và có giá trị nhỏ nhất khi là -1 khi x=2
Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x-2018)-2|=m có đúng 3 nghiệm.
Cho hàm số y f(x) xác định, liên tục trên R và có bảng biến thiên sauTìm tất cả các giá trị thực của tham số m để phương trình f(x) - 1 m có đúng hai nghiệm. A.
m
-
2
,
m
≥
-
1
B.
m
0
,
m
-
1
C.
m
-
...
Đọc tiếp
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên sau
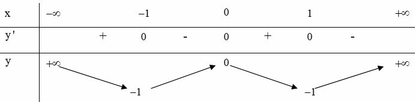
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) - 1 = m có đúng hai nghiệm.
A. m = - 2 , m ≥ - 1
B. m > 0 , m = - 1
C. m = - 2 , m > - 1
D. - 2 < m < - 1
Cho hàm số y f(x) xác định, liên tục trên R và có bảng biến thiên sauTìm tất cả các giá trị thực của tham số m để phương trình f(x) - 1 m có đúng hai nghiệm A.
m
-
2
,
m
≥
-
1
B.
m
0
,
m
-
1
C.
m
-
2
,
...
Đọc tiếp
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên sau
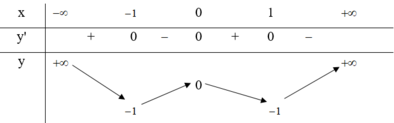
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) - 1 = m có đúng hai nghiệm
A. m = - 2 , m ≥ - 1
B. m > 0 , m = - 1
C. m = - 2 , m > - 1
D. - 2 < m < - 1
Cho hàm số y f(x) xác định trên R và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình 2
f
(
x
)
- m 0 có đúng bốn nghiệm phân biệt. A. 0 m 8 B.m 4 C.m 0 ; m 8 D. -2 m 4
Đọc tiếp
Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình
2 f ( x ) - m = 0 có đúng bốn nghiệm phân biệt.
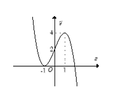
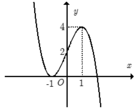
A. 0< m< 8
B.m> 4
C.m< 0 ; m> 8
D. -2< m< 4
+ Trước tiên từ đồ thị hàm số y= f( x) , ta suy ra đồ thị hàm số y = |f(x)| như hình dưới đây:

Phương trình 2|f(x)| - m = 0 hay |f(x)| = m/2 là phương trình hoành độ giao điểm của đồ thị hàm số y = |f(x) và đường thẳng y= m/2.
Dựa vào đồ thị hàm số y = |f(x)|, ta có ycbt trở thành:
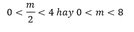
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định, liên tục trên R và có bảng biến thiên sauTìm tất cả các giá trị thực của tham số m để phương trình yf(x)-1m có đúng hai nghiệm A.
m
-
2
,
m
≥
-
1
.
B.m0,m-1 C.m-2,m-1 D.-2m-1
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên sau
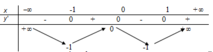
Tìm tất cả các giá trị thực của tham số m để phương trình yf(x)-1=m có đúng hai nghiệm
A. m = - 2 , m ≥ - 1 .
B.m>0,m=-1
C.m=-2,m>-1
D.-2<m<-1
Cho hàm số y f(x) xác định, liên tục trên R và có bảng biến thiên sau: Tìm tất cả các giá trị thực của tham số m để phương trình y f(x) - 1 có đúng hai nghiệm. A. m 2, m
≥
-1 B. m 0, m -1 C. m -2; m -1 D. -2 m -1
Đọc tiếp
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên sau:

Tìm tất cả các giá trị thực của tham số m để phương trình y = f(x) - 1 có đúng hai nghiệm.
A. m = 2, m ≥ -1
B. m > 0, m = -1
C. m = -2; m > -1
D. -2 < m < -1
Chọn C.
f(x) - 1 = m![]()
Dựa vào bảng biến thiên, để phương trình f(x) - 1 có đúng hai nghiệm thì
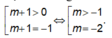
Đúng 0
Bình luận (0)