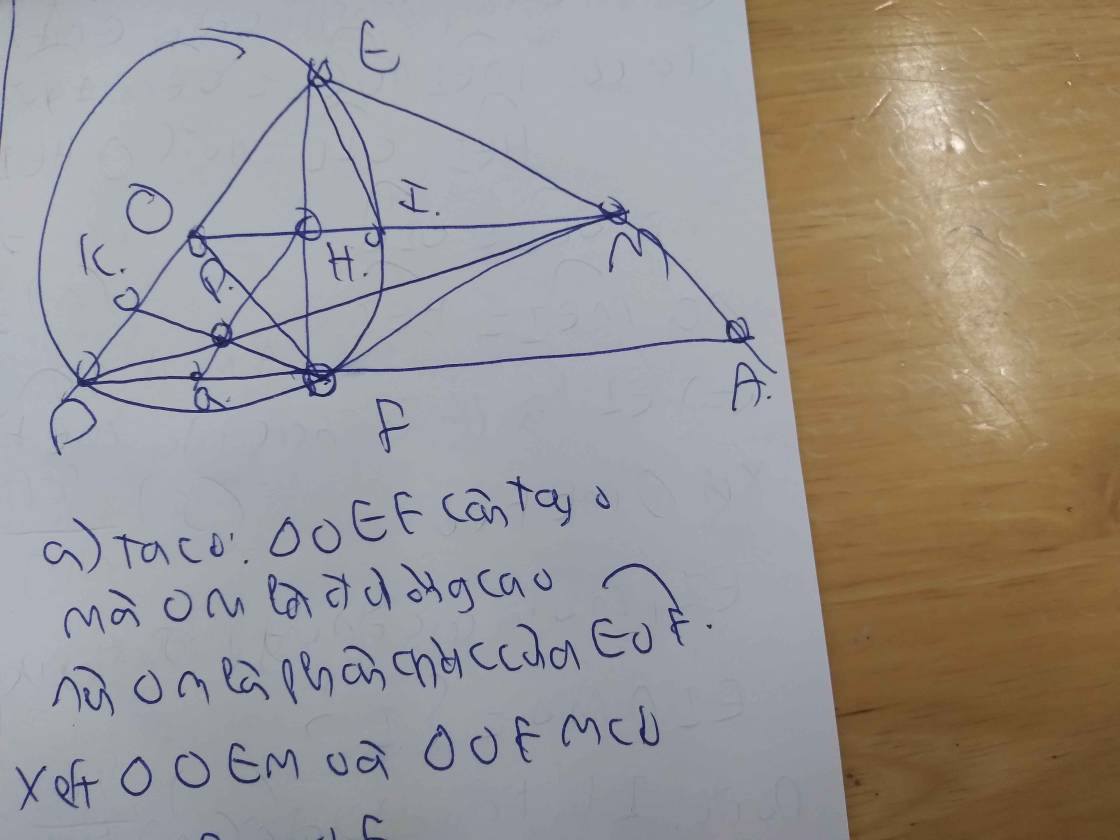
Cho đường tròn tâm O , bán kính R , từ điểm M nằm ngoài đường tròn, kẻ tiếp tuyến ME, MF đến đường tròn
â) Cm: 4 điểm M,E,O,F thuộc đường tròn
b) Đoạn OM cắt đường tròn tâm O tại I . CM: I là tâm đường tròn nội tiếp tam giác MEF
c) Kẻ đường kính ED của đường tròn tâm O . Kẻ FK vuông góc ED . Gọi P là giao điểm của MD và KF. CM: P là trung điểm FK
CHỈ CẦN LÀM GIÚP MÌNH LÀM CẦU (C) LÀ ĐƯỢC RỒI