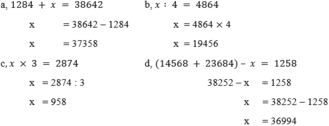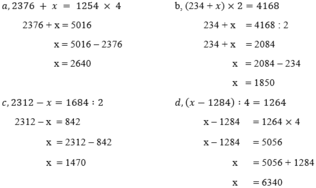\(3^{99}=\left(3^3\right)^{33}=27^{33}>27^{21}>11^{21}\\ 16^x< 128^4\\ \Rightarrow\left(2^4\right)^x< \left(2^7\right)^4\\ \Rightarrow2^{4x}< 2^{28}\Rightarrow4x< 28\Rightarrow x< 7\)

Đáp án là B

B nha~

Hok tốt~

Ta có : \(16^x=1284\)

\(\Rightarrow x\in\left\{0;1;2\right\}\)

Vậy x = 0 ; 1 ; 2

\(16^x< 128^4\)

\(\Rightarrow\left(2^4\right)^x< \left(2^7\right)^4\)

\(\Rightarrow2^{4.x}< 2^{7.4}\)

\(\Rightarrow2^{4.x}< 2^{28}\)

\(\Rightarrow4.x< 28\)

\(\Rightarrow\)4.x= 0; 4 ; 8 ; 12 ; 16 ; 20 ; 24

\(\Rightarrow\)x= 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6

Chúc Quốc Bảo học tốt.

x ko nhận giá trị nào

Tìm x

Tìm x:

Tìm x

√16x = 8 (điều kiện: x ≥ 0)

⇔ 16x = 82 ⇔ 16x = 64 ⇔ x = 4

(Hoặc: √16x = 8 ⇔ √16.√x = 8

⇔ 4√x = 8 ⇔ √x = 2 ⇔ x = 4)

`3-16x^2=0`

`<=>(\sqrt3)^2-(4x)^2=0`

`<=>(\sqrt3+4x)(\sqrt3-4x)=0`

`<=> [(\sqrt3=-4x),(\sqrt3=4x):}`

`<=> [(x=-\sqrt3/4),(x=\sqrt3/4):}`

Vậy `S={\pm \sqrt3/4}`.

Ta có: \(3-16x^2=0\)

\(\Leftrightarrow16x^2=3\)

\(\Leftrightarrow x^2=\dfrac{3}{16}\)

hay \(x\in\left\{\dfrac{\sqrt{3}}{4};-\dfrac{\sqrt{3}}{4}\right\}\)

\(\sqrt{x-3}-\sqrt{9x-27}+2\sqrt{16x-48}=6\)

\(\Leftrightarrow\sqrt{x-3}=1\)

hay x=4

x,y nguyên à bạn hay x,y là số thực?

có 2 cách làm nhe

C1: thay y = 0 để tìm x 

ta sẽ có : \(16x^2=3^0+143\)

\(\Leftrightarrow16x^2=1+143\)

\(\Leftrightarrow16x^2=144\)

\(\Leftrightarrow x^2=144:16=9\)

\(\Leftrightarrow x=\sqrt{9}=3\) hoặc -3 

cách này chắc sẽ được hơn vs cách 2 vì chương trình lớp 6 chưa học tới tách biến và lôgarit , mà bạn cứ tham khảo thêm c2 nha

C2:

bằng phương pháp tách biến , chia mỗi vế cho các nhân tử khong chứa biến.

\(x=\pm\dfrac{\sqrt{3^y+143}}{4}\)

sử dụng lôgarit :

\(y=\dfrac{ln\left(16x^2-143\right)}{ln\left(3\right)}\)