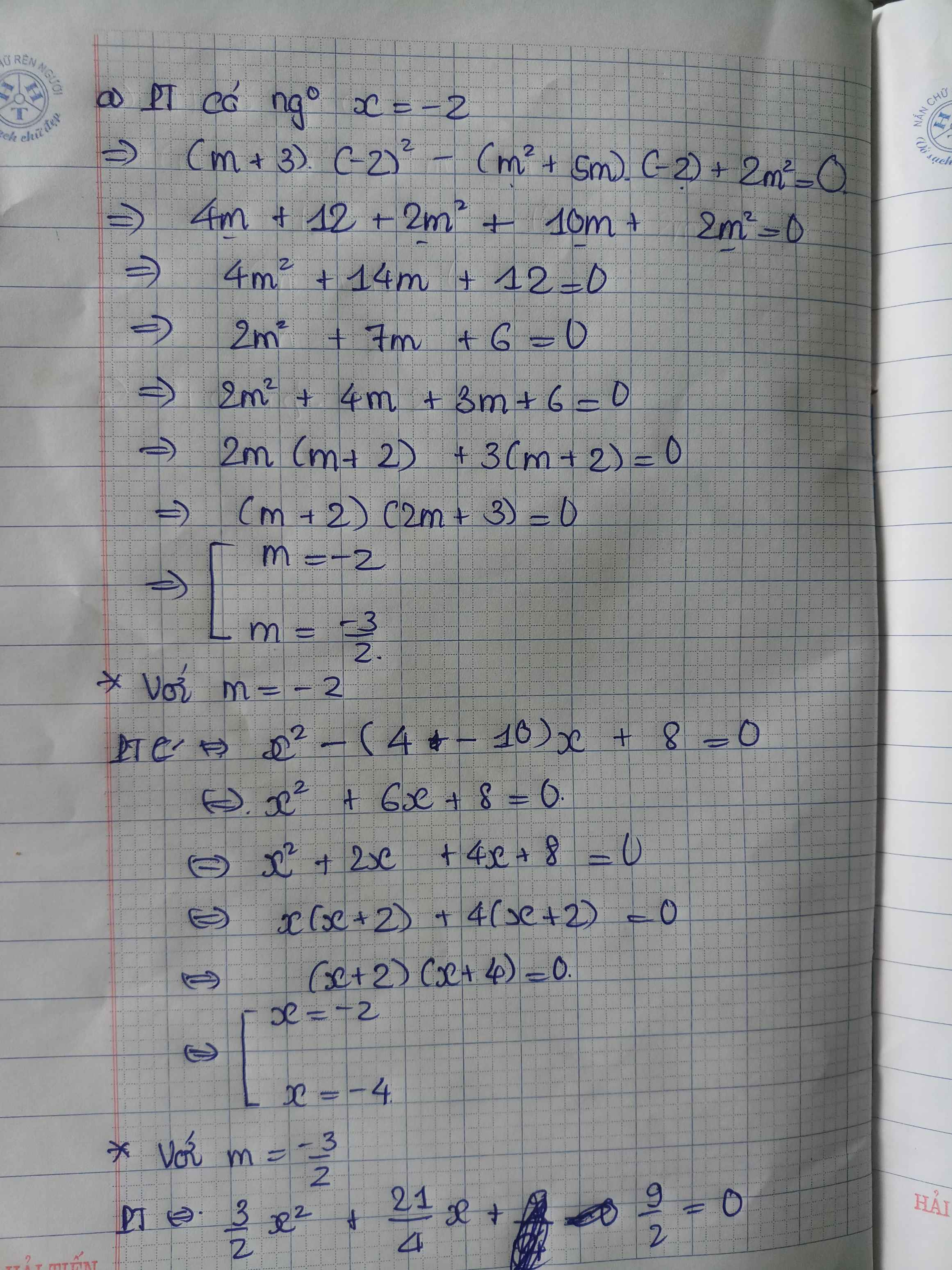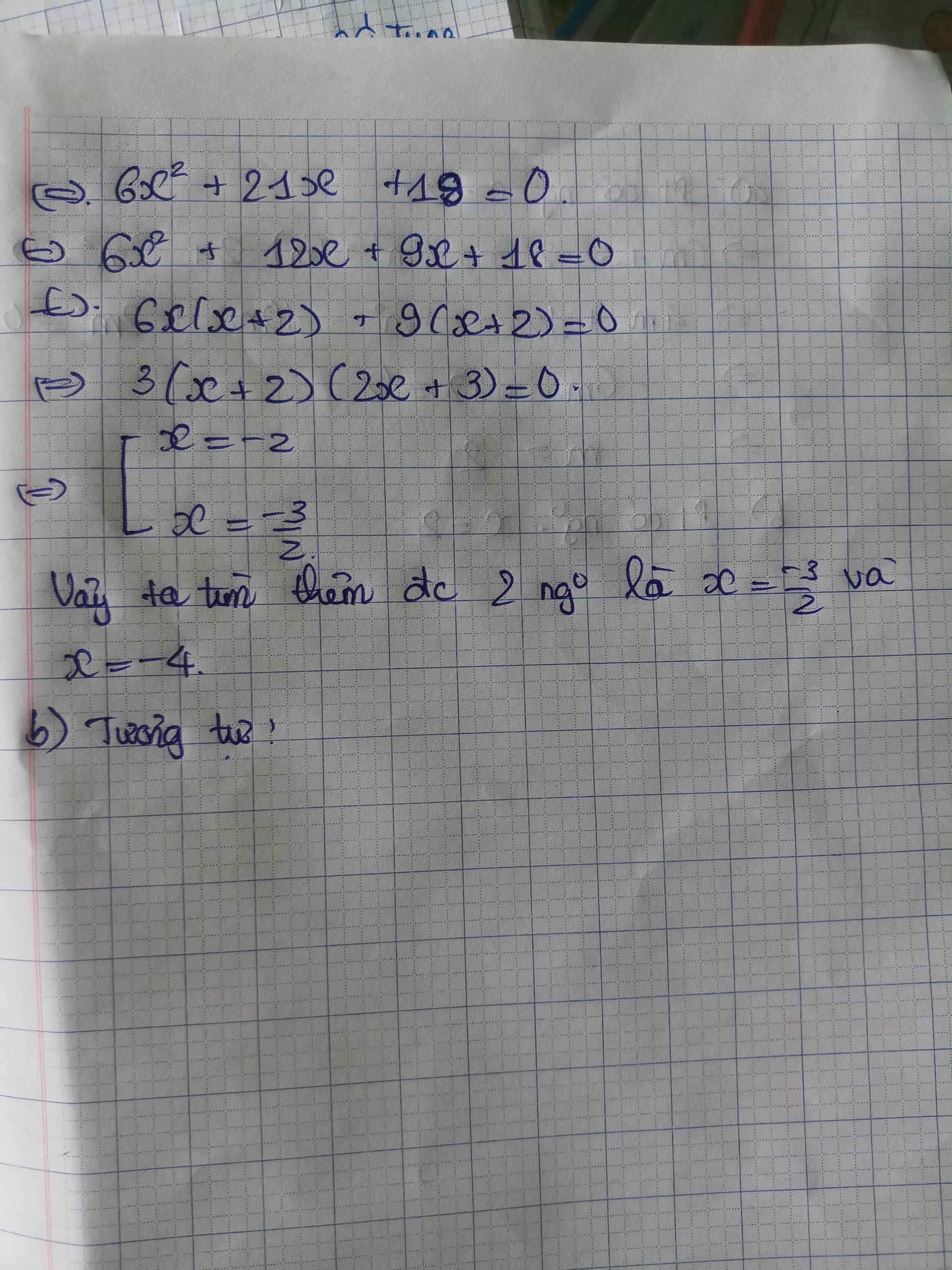b) Thay x=2 vào pt, ta được:

\(4\left(m^2-1\right)-4m+m^2+m+4=0\)

\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)

\(\Leftrightarrow5m^2-3m=0\)

\(\Leftrightarrow m\left(5m-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)

Áp dụng hệ thức Vi-et, ta được:

\(x_1+x_2=\dfrac{2m}{m^2-1}\)

\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)

1.

\(\left\{{}\begin{matrix}\left(x^2-2x\right)\left(y^2-6y\right)=m\\\left(x^2-2x\right)+\left(y^2-6y\right)=3m\end{matrix}\right.\)

Theo Viet đảo, \(x^2-2x\ge-1\) và \(y^2-6y\ge-9\) là nghiệm của:

\(t^2-3m.t+m=0\) (1) 

Hệ đã cho có đúng 3 nghiệm khi và chỉ khi:

TH1: (1) có 1 nghiệm \(t_1=-1\) và 1 nghiệm \(t_2>-9\)

\(t=-1\Rightarrow1+3m+m=0\Rightarrow m=-\dfrac{1}{4}\)

\(\Rightarrow t_2=\dfrac{1}{4}\) (thỏa mãn)

TH2: (1) có 1 nghiệm \(t_1=-9\) và 1 nghiệm \(t_2>-1\)

\(t_1=-9\Rightarrow81+27m+m=0\Leftrightarrow m=-\dfrac{81}{28}\)

\(\Rightarrow t_2=\dfrac{9}{28}\) (thỏa mãn)

Vậy \(m=\left\{-\dfrac{1}{4};-\dfrac{81}{28}\right\}\)

2. Pt bậc 2 có nghiệm duy nhất thì nó là nghiệm kép

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(m+3\right)^2-4\left(2m-1\right)=0\left(vô-nghiệm\right)\\\dfrac{m+3}{2}\le3\end{matrix}\right.\)

Ko tồn tại m thỏa mãn

Hoặc là ngôn ngữ đề bài có vấn đề, ý của người ra đề là "phương trình đã cho có 2 nghiệm, trong đó có đúng 1 nghiệm thỏa mãn \(x\le3\)"?

- Với \(m=\dfrac{1}{2}\) ko thỏa mãn

- Với \(m\ne\dfrac{1}{2}\)

\(\Leftrightarrow\left(2m-1\right)x^3-\left(2m-1\right)x^2-\left(m-2\right)x^2+\left(m-4\right)x+2\ge0\)

\(\Leftrightarrow\left(2m-1\right)x^2\left(x-1\right)-\left(x-1\right)\left[\left(m-2\right)x+2\right]\ge0\)

\(\Leftrightarrow\left(x-1\right)\left[\left(2m-1\right)x^2-\left(m-2\right)x-2\right]\ge0\) (1)

Do (1) luôn chứa 1 nghiệm \(x=1\in\left(0;+\infty\right)\) nên để bài toán thỏa mãn thì cần 2 điều sau đồng thời xảy ra:

+/ \(2m-1>0\Rightarrow m>\dfrac{1}{2}\)

+/ \(\left(2m-1\right)x^2-\left(m-2\right)x-2=0\) có 2 nghiệm trong đó \(x_1\le0\) và \(x_2=1\)

Thay \(x=1\) vào ta được:

\(\left(2m-1\right)-\left(m-2\right)-2=0\Leftrightarrow m=1\)

Khi đó: \(x^2+x-2=0\) có 2 nghiệm \(\left[{}\begin{matrix}x_1=-2< 0\left(thỏa\right)\\x_2=1\end{matrix}\right.\)

Vậy \(m=1\)

ĐK; \(-1\le x\le3\)

Đặt \(\sqrt{-x^2+2x+3}=t\left(0\le t\le2\right)\)

\(pt\Leftrightarrow m+1=-x^2+2x+3+4\sqrt{-x^2+2x+3}\)

\(\Leftrightarrow m+1=f\left(t\right)=t^2+4t\)

\(f\left(0\right)=0;f\left(2\right)=12\)

Yêu cầu bài toán thỏa mãn khi \(minf\left(t\right)\le m+1\le maxf\left(t\right)\)

\(\Leftrightarrow0\le m+1\le12\)

\(\Leftrightarrow-1\le m\le11\)

\(a,\Leftrightarrow\Delta'\ge0\\ \Leftrightarrow\left(m+2\right)^2-\left(m^2-4\right)\ge0\\ \Leftrightarrow m^2+4m+4-m^2+4\ge0\\ \Leftrightarrow4m+8\ge0\\ \Leftrightarrow m\ge-2\\ b,\Leftrightarrow\Delta'=0\Leftrightarrow m=-2\)

x = 10 do ban 

bạn giải cụ thể ra đc k 

a: \(\text{Δ}=\left(2m-2\right)^2-4\left(2m-3\right)\)

\(=4m^2-8m+4-8m+12\)

\(=4m^2-16m+16\)

\(=\left(2m-4\right)^2>=0\)

Do đó: Phương trình luôn có nghiệm

b: Để phương trình có hai nghiệm trái dấu thì 2m-3<0

hay m<3/2

c: Để phương trình có hai nghiệm sao cho nghiệm này gấp đôi nghiệm kia thì ta có hệ phương trình:

\(\left\{{}\begin{matrix}x_1-2x_2=0\\x_1+x_2=2m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x_2=-2m+2\\x_1=2x_2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{2m-2}{3}\\x_1=\dfrac{4m-4}{3}\end{matrix}\right.\)

Ta có: \(x_1x_2=2m-3\)

\(\Leftrightarrow2m-3=\dfrac{2m-2}{3}\cdot\dfrac{4m-4}{3}\)

\(\Leftrightarrow8\left(m-1\right)^2=9\left(2m-3\right)\)

\(\Leftrightarrow8m^2-16m+8-18m+27=0\)

\(\Leftrightarrow8m^2-34m+35=0\)

\(\text{Δ}=\left(-34\right)^2-4\cdot8\cdot35=36>0\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}m_1=\dfrac{34-6}{16}=\dfrac{28}{16}=\dfrac{7}{4}\\m_2=\dfrac{34+6}{16}=\dfrac{40}{16}=\dfrac{5}{2}\end{matrix}\right.\)