chứng minh45-83+26chia hết cho 9
giúp mình nhé
thanks
cho mình lời giải
1028+8/chứng tỏ chia hết cho 9
giúp mình với
TL:
Ta có: \(10^{28}+8=100...00\)(\(28\) chữ số \(0\)) \(+8⋮9\) ( Vì \(1+8=9⋮9\))
Vậy\(10^{28}+8⋮9\) thoả mãn bài toán
CHÚC BẠN HỌC TỐT NHÉ.
1028 + 8 chia hết cho 9
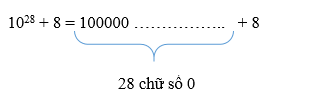
1028 + 8 = 1 + 0 + 0 + ............... + 8 = 9
Mà \(9⋮9\)
\(\Rightarrow10^{28}+8⋮9\)
(2x + 1)^2 = 9
giúp mình nhé mình tick cho nếu cau trả lời đúng
`(2x+1)^2=9`
`(2x+1)^2=3^2=(-3)^2`
TH1: `2x+1=3`
`2x=2`
`x=1`
TH2: `2x+1=-3`
`2x=-4`
`x=-2`
(2x + 1)2 = 9
(2x + 1)2 = 32
\(\Rightarrow\)Trường hợp 1:
2x + 1 = 3
2x = 3 - 1
2x = 2
x = 2 : 2
x = 1
Trường hợp 2:
2x + 1 = -3
2x = -3 - 1
2x = -4
x = -4 : 2
x = -2
x \(\in\) \(\left\{-2;1\right\}\)
Ta có: \(\left(2x+1\right)^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=3\\2x+1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Tìm các chữ số a,b trong số 21ab chia hết cho 83
Mình đang cần gấp, bạn nào trả lời nhanh nhất mà có lời giải mình sẽ tích cho!
Gọi thương của phép chia 21ab cho 83 là a \(\left(a\in N\right)\)
Ta có :
\(2100\div83\approx25,3;2200\div83\approx26,5\)
Vì : \(25,3< a< 26,5\)và \(a\in N\)nên a = 26
Khi đó : \(21ab=26.83=2158\)
\(\Rightarrow ab=58\)
Vậy a = 5 ; b = 8
Nguyễn Thiện Nhân, bạn trả lời thế nào mình không hiểu?
24 : 3=........=..........
a.24/3 b.8 c.9
giúp mình nhé, trả lời mik tick cho nha
24 : 3=........=..........
a.24/3 b.8 c.9
Cho 3a + 2b chia hết cho 17 ( a, b thuộc N ). Chứng minh rằng: 10a + b chia hết cho 17
Mình đang cần câu trả lời rất gấ..........................p , ai tả lời đúng và nhanh nhất mình tick cho ( nhớ có lời giải nữa nha)
| Cho tổng S = 3^1+ 3^2+3^3 + ...+ 3^20 . Chứng tỏ: |
| a) S chia hết 12 | b) S chia hết 120 |
Các bạn cho mình lời giải chi tiết nha. Mình cảm ơn^^
\(a,S=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{19}+3^{20}\right)\\ S=\left(3+3^2\right)+3^2\left(3+3^2\right)+...+3^{18}\left(3+3^2\right)\\ S=\left(3+3^2\right)\left(1+3^2+...+3^{18}\right)=12\left(1+3^2+...+3^{18}\right)⋮12\)
\(b,S=\left(3+3^2+3^3+3^4\right)+...+\left(3^{17}+3^{18}+3^{19}+3^{20}\right)\\ S=\left(3+3^2+3^3+3^4\right)+....+3^{16}\left(3+3^2+3^3+3^4\right)\\ S=\left(3+3^2+3^3+3^4\right)\left(1+...+3^{16}\right)\\ S=120\left(1+...+3^{16}\right)⋮120\)
\(a,S=3+3^2+3^3+...+3^{20}\)
Ta thấy:\(3+3^2=12⋮12\)
\(\Rightarrow S=\left(3+3^2\right)+3^2\left(3+3^2\right)+...+3^{18}\left(3+3^2\right)\\ \Rightarrow S=\left(3+3^2\right)\left(1+3^2+...+1^{18}\right)\\ \Rightarrow S=12.\left(1+3^2+...+3^{18}\right)⋮12\\ \left(đpcm\right)\)
\(b,Ta\) \(thấy:\)\(3+3^2+3^3+3^4=120⋮120\)
\(\Rightarrow S=\left(3+3^2+3^3+3^4\right)+...+\left(3^{17}+3^{18}+3^{19}+3^{20}\right)\\ \Rightarrow S=\left(3+3^2+3^3+3^4\right)+...+3^{16}\left(3+3^2+3^3+3^4\right)\\ \Rightarrow S=\left(3+3^2+3^3+3^4\right)\left(1+...+3^{16}\right)\\ \Rightarrow S=120\left(1+...+3^{16}\right)⋮120\\ \left(đpcm\right)\)
hãy chứng tỏ ab+ba chia hết cho 11
viết cả lời giải cho mình nhé
xét: ab + ba = 10a + b + 10b + a = ( 10a+ a ) + ( 10b + b )
= 11a + 11 b = 11.( a + b ) chia hết cho 11
vậy: ab + ba chia hết cho 11 ( đpcm )
ab + ba
= 10a + b + 10b + a
=11a + 11b
= 11(a + b) chia hết cho 11
Vậy ab + ba chia hết cho 11
k mk nha
cho một h.thang vuông ABCD vuông góc tại A và D, đáy lớn CD dài hơn đáy bé AB là 3,5 cm và đáy CD = 5/4 đáy AB, cạnh AD dài 10cm. Trên AD lấy điểm E sao cho DE= 3cm. Từ E kẻ đường thẳng song song với hai đáy hình thang cắt BC tại G.
a. Tính d. tích h.thang ABCD
b. tính độ dài đoạn EG.
Giúp nhé!
Chứng minh rằng
1025_ 26chia hết cho 9 và 2
5n_1 chia hết cho 4
10n_ 1 chia hết cho 9
10n +8 chia hết cho 9
b: \(5^n-1=\left(5-1\right)\cdot A=4\cdot A⋮A\)
c: \(10^n-1=\left(10-1\right)\cdot B=9\cdot B⋮9\)
d: \(10^n+8=10....08⋮9\)
B=3+32+33+...+3120. Chứng minh rằng:
a)B chia hết cho 3
b)B chia hết cho 4
c)B chia hết cho 13
Mọi người cho mình lời giải chi tiết nhé.
a: \(B=3+3^2+3^3+...+3^{120}\)
\(=3\left(1+3+3^2+...+3^{119}\right)⋮3\)
b: \(B=3+3^2+3^3+3^4+...+3^{2020}\)
\(=3\left(1+3\right)+...+3^{2019}\left(1+3\right)\)
\(=4\cdot\left(3+...+3^{2019}\right)⋮4\)