biết sina=2/3.Tính giá trị biểu thức:A=2sin2a+5cos2a

Những câu hỏi liên quan
Tính giá trị biểu thức
D=\(\dfrac{cosa+sina}{cosa-sina}\) biết tan α =\(\dfrac{1}{2}\)
Chia cả tử và mẫu cho \(cosa\)
\(D=\dfrac{\dfrac{cosa}{cosa}+\dfrac{sina}{cosa}}{\dfrac{cosa}{cosa}-\dfrac{sina}{cosa}}=\dfrac{1+tana}{1-tana}=\dfrac{1+\dfrac{1}{2}}{1-\dfrac{1}{2}}=3\)
Đúng 1
Bình luận (0)
Tính giá trị biểu thức P ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b
π
4
Đọc tiếp
Tính giá trị biểu thức P = ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b = π 4
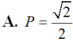
![]()
![]()
![]()
Chọn C.
Theo giả thiết ta có:
P = ( sina + sinb) 2 + ( cosa + cosb) 2
= sin2a + 2.sina.sinb + sin2b + cos2a + 2cosa. cosb + cos2b
= 2 + 2( sina.sinb + cos a. cosb)
= 2 + 2.cos( a - b) ( sử dụng công thức cộng)
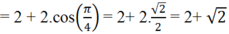
Đúng 0
Bình luận (0)
Tính giá trị biểu thức:
a) 2. |- 21| - 3 . |125| - 5 . |-33| - |2. 21|
\(2\cdot\left|-21\right|-3\cdot\left|125\right|-5\cdot\left|-33\right|-\left|2\cdot21\right|\)
\(=2\cdot21-3\cdot125-5\cdot33-2\cdot21\)
\(=-3\cdot125-5\cdot33=-375-165=-540\)
Đúng 0
Bình luận (0)
Tính giá trị nhỏ nhất của biểu thức:
A= 2x\(^2\) + 2\(\sqrt{2x}\) + 3
\(A=2x^2+2\sqrt{2}x+3\\ =2\left(x^2+\sqrt{2}x+\dfrac{3}{2}\right)\\ =2.\left(x^2+2.\dfrac{1}{\sqrt{2}}x+\dfrac{1}{2}+1\right)\\ =2.\left(x^2+2.\dfrac{1}{\sqrt{2}}x+\dfrac{1}{2}\right)+2\\ =2.\left(x+\dfrac{1}{\sqrt{2}}\right)^2+2\)
Ta có \(2.\left(x+\dfrac{1}{\sqrt{2}}\right)^2\ge0\forall x\)
\(2.\left(x+\dfrac{1}{\sqrt{2}}\right)^2+2\ge2\forall x\)
Dấu bằng xảy ra khi : \(x+\dfrac{1}{\sqrt{2}}=0\\ \Rightarrow x=\dfrac{-\sqrt{2}}{2}\)
Vậy \(Min_A=2\) khi \(x=\dfrac{-\sqrt{2}}{2}\)
Đúng 2
Bình luận (0)
Tính giá trị của biểu thức:
a) 96 : 3 x 5 b) 60 : (2 x 3)
a) 96 : 3 x 5 = 32 x 5 = 160 | b) 60 : (2 x 3) = 60 : 6 = 10 |
Đúng 0
Bình luận (0)
Tính giá trị biểu thức:A=x33+x2y-2x2-xy-y2+3y+x-5. Biết x+y-2=0
Tính giá trị biểu thức:A=4x^4+7x^2y^2+3y^4+5y^2 biết x^2+y^2
câu20:Cho tana=-2 và pi/2<a<pi.Tính giá trị biểu thức P=cos2a+sin2a
câu21Cho 2tana-cota=1 và -pi/2<a<0.Tính giá trị của biểu thức P=tana+2cota
câu22: Cho sina=-1/7 và pi<a<3pi/2.Tính giá trị của biểu thức P=cos(a+pi/6)
câu23: Cho sina=-1/9; cosb=-2/3 và pi<a<3pi/2; pi/2<b<pi. Tính giá trị của biểu thức P= sin(a+b)
Tính giá trị biểu thức:
a) 6 : 5/2 - 3/10
b) 4/6 : 4/3 + 5 : 4/3
a. 7/2 - 3/10 = 16/5
b. (4/6 + 5):4/3=17/3 :4/3=17/4
Đúng 0
Bình luận (0)
a) \(6-\dfrac{5}{2}-\dfrac{3}{10}=\dfrac{7}{2}-\dfrac{3}{10}=\dfrac{16}{5}\)
b) \(\dfrac{4}{6}\div\dfrac{4}{3}+5\div\dfrac{4}{3}\)
\(=\dfrac{1}{2}+\dfrac{15}{4}\)
\(=\dfrac{17}{4}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời























