Cho tam giác ABC có 4vecto CA+ 3vecto CB = vecto 0 . Xác định điểm I cho I thuộc AB

Những câu hỏi liên quan
2. CHO HÌNH BÌNH HÀNH ABCD CÓ O LÀ GIAO ĐIỂM CỦA AC VÀ BD CHỨNG MINH RẰNG
A, VỚI MỌI ĐIỂM M TA CÓ VECTO MA + VECTO MB + VECTO MC + VECTO MD = 4VECTO MO
B, VECTO AB+ 2VECTO AC + VECTO AD = 3VECTO AC
5. CHO ĐOẠN THẲNG AB VÀ ĐIỂM I SAO CHO 2VECTO AI + 3VECTO IB = VECTO 0
TÌM K SAO CHO VECTO AI = K VECTO AB
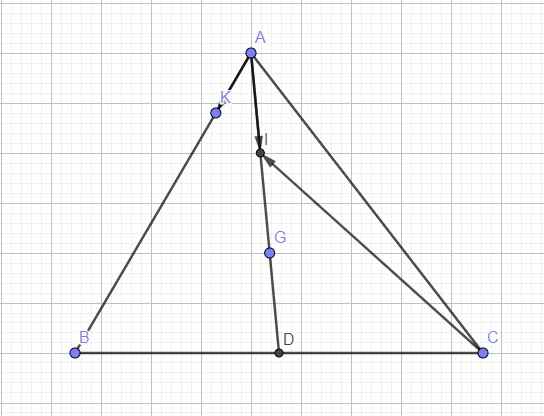
Cho tam giác ABC có trung tuyến AD, trọng tâm G, I là trung điểm AG, K thuộc đoạn AB. AK=1/5 AB, phân tích các vecto sau qua vecto CA, vecto CB a. Vecto AI b. Vecto AK c. Vecto CI d. Vecto CK
Do G là trọng tâm tam giác
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}=-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
Do I là trung điểm AG
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)=-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AB}=\dfrac{1}{5}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
\(\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{CA}-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}=\dfrac{4}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC và I thỏa mãn vecto IA=3vecto IB. Phân tích vecto CI theo vecto CA và vecto CB
Gọi M là trung điểm của AB
Ta có:\(\overrightarrow{CI}=\frac{\overrightarrow{CM}+\overrightarrow{CB}}{2}=\frac{\frac{\overrightarrow{CA}+\overrightarrow{CB}}{2}+\overrightarrow{CB}}{2}=\frac{1}{4}\overrightarrow{CA}+\frac{3}{4}\overrightarrow{CB}\)
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy cho A(2;4);B(1;1);C(1;-3)
1.a)xác định tọa độ điểm M sao cho vecto MA- vecto CB =2 lần vecto MC.
b)tìm tọa độ điểm D thuộc trục Ox sao cho tam giác ABD vuông tại B.
2.cho tam giác ABC có AB=2 ;CA=3.gọi G là trọng tâm tam giác ABC .tính tích vecto AG và BC.
giúp mk nha 5 sao cho người nhanh nhất
có ai biết cách làm thì giúp mk với mai mk cần lắm rồi
Đúng 0
Bình luận (0)
Cho tan giác ABC đều cạnh a, I là điểm trên cạnh BC sao cho BC 3BI và J là trung điểm của AB.
a) Tính |vecto AB + vecto AC|
b) Chứng minh vecto AI 2/3vecto AB + 1/2vecto AC.
c) Gọi M là điểm thoả : 3vecto MA + vecto MB - 2vecto MC vecto 0.
d) Gọi N là điểm thoả : |vecto NA + vecto NB| |vecto NB + vecto NC. Chứng minh điểm N thuộc một đường thẳng cố định.
giúp mình với ạ :((
Đọc tiếp
Cho tan giác ABC đều cạnh a, I là điểm trên cạnh BC sao cho BC = 3BI và J là trung điểm của AB.
a) Tính |vecto AB + vecto AC|
b) Chứng minh vecto AI = 2/3vecto AB + 1/2vecto AC.
c) Gọi M là điểm thoả : 3vecto MA + vecto MB - 2vecto MC = vecto 0.
d) Gọi N là điểm thoả : |vecto NA + vecto NB| = |vecto NB + vecto NC. Chứng minh điểm N thuộc một đường thẳng cố định.
giúp mình với ạ :((
Cho tam giác ABC có M là trung điểm của trung tuyến AD, N là điểm thỏa mãn hệ thức: 3vecto AN=vectoAC
a) Chứng minh rằng 3 điểm B, M, N thẳng hàng.
b) Trên AB lấy điểm I sao cho vecto AI=2/3AB, trên AC lấy điểm J sao cho vecto AJ=2/5 vecto AC .
Chứng minh rằng 3 điểm I, M, J thẳng hàng.
giúp em làm phần b với ạ,,em cần gấp ạ
Tìm điểm I sao cho: | 2vecto IA+ 3vecto IB + 4vecto IC|=0
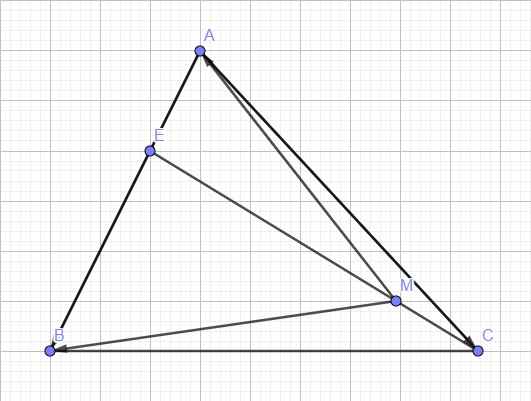
Bài 14. Cho tam giác ABC. Trên cạnh AB lấy điểm E sao cho EB = 2EA; M là điểm thỏa mãn vecto ME + 3vecto MC =vecto 0. Biểu diễn vectơ MA qua các vectơ MB , MC .
\(\overrightarrow{ME}+3\overrightarrow{MC}=\overrightarrow{0}\Rightarrow\overrightarrow{MC}=-\dfrac{1}{3}\overrightarrow{ME}\)
\(EB=2EA\Rightarrow\overrightarrow{BE}=2\overrightarrow{EA}\)
Ta có: \(\overrightarrow{ME}=\overrightarrow{MB}+\overrightarrow{BE}=\overrightarrow{MB}+2\overrightarrow{EA}=\overrightarrow{MB}+2\left(\overrightarrow{EM}+\overrightarrow{MA}\right)=\overrightarrow{MB}-2\overrightarrow{ME}+2\overrightarrow{MA}\)
\(\Rightarrow3\overrightarrow{ME}=\overrightarrow{MB}+2\overrightarrow{MA}\Rightarrow\overrightarrow{ME}=\dfrac{1}{3}\overrightarrow{MB}+\dfrac{2}{3}\overrightarrow{MA}\)
\(\Rightarrow\overrightarrow{MC}=-\dfrac{1}{3}\overrightarrow{ME}=-\dfrac{1}{9}\overrightarrow{MB}-\dfrac{2}{9}\overrightarrow{MA}\)
\(\Rightarrow\dfrac{2}{9}\overrightarrow{MA}=-\dfrac{1}{9}\overrightarrow{MB}-\overrightarrow{MC}\Rightarrow\overrightarrow{MA}=-\dfrac{1}{2}\overrightarrow{MB}-\dfrac{9}{2}\overrightarrow{MC}\)
Đúng 2
Bình luận (0)
cho tam giác ABC bất kì , gọi M,N,P lần lượt là trung điểm các cạnh AB,BC,CA . H,H' lần lượt là trực tâm của tam giác ABC,MNP. .Khẳng định nào sau đây đúng?
A) vecto HA + vecto HB + vecto HC = 3vecto HH'
B) vecto HA + vecto HB + vecto HC = 2vecto HH'
C) vecto HA + vecto HB + vecto HC = vecto 0
D) vecto HM + vecto HN + vecto HP = 3vecto HH'
Lời giải:
Có thể loại ngay đáp án C vì nếu $H\equiv G$( $G$ là trọng tâm $ABC$) thì ta mới có công thức trên.
$\overrightarrow{HM}+\overrightarrow{HN}+\overrightarrow{HP}=\frac{1}{2}(2\overrightarrow{HM}+2\overrightarrow{HN}+2\overrightarrow{HP})$
$=\frac{1}{2}(\overrightarrow{HA}+\overrightarrow{AM}+\overrightarrow{HB}+\overrightarrow{BM})+\overrightarrow{HB}+\overrightarrow{BN}+\overrightarrow{HC}+\overrightarrow{CN}+\overrightarrow{HC}+\overrightarrow{CP}+\overrightarrow{HA}+\overrightarrow{AP})$
$=\frac{1}{2}(2\overrightarrow{HA}+2\overrightarrow{HB}+2\overrightarrow{HC})=\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}$ nên 2 phương án A, D tương đương nhau.
Do đó có thể suy ra đáp án B là đáp án đúng.
Đúng 0
Bình luận (0)
Nếu bạn muốn chứng minh hẳn tại sao đáp án B đúng thì có thể làm như sau:
Dễ thấy $\triangle ABC\sim \triangle NPM$ theo tỷ lệ $2$
Mà $H, H'$ lần lượt là trực tâm 2 tam giác trên
$\Rightarrow \frac{CH}{MH'}=2$
$\Leftrightarrow CH=2MH'(1)$
Mặt khác: $CH\perp AB; MH'\perp PN; AB\parallel PN$ nên $MH'\parallel CH(2)$
Từ $(1); (2)\Rightarrow 2\overrightarrow{H'M}=\overrightarrow{CH}$
Từ đây ta có:
$\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{HH'}+\overrightarrow{H'A}+\overrightarrow{HH'}+\overrightarrow{H'B}+\overrightarrow{HC}$
$=2\overrightarrow{HH'}+(\overrightarrow{H'A}+\overrightarrow{H'B})+\overrightarrow{HC}$
$=2\overrightarrow{HH'}+(\overrightarrow{H'A}+\overrightarrow{AM}+\overrightarrow{H'B}+\overrightarrow{BM})+\overrightarrow{HC}$
$=2\overrightarrow{HH'}+(\overrightarrow{H'M}+\overrightarrow{H'M})+\overrightarrow{HC}$
$=2\overrightarrow{HH'}+2\overrightarrow{H'M}+\overrightarrow{HC}$
$=2\overrightarrow{HH'}+\overrightarrow{CH}+\overrightarrow{HC}$
$=2\overrightarrow{HH'}$
Vậy đáp án B đúng.
Đúng 0
Bình luận (0)