giúp mk gấp
phát biểu định lí
Cho các mệnh đề
P: “a và b chia hết cho c”;
Q: “a + b chia hết cho c”.
a) Hãy phát biểu định lí \(P \Rightarrow Q\). Nêu giả thiết, kết luận của định lí và phát biểu định lí này dưới dạng điều kiện cần, điều kiện đủ.
b) Hãy phát biểu mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) rồi xác định tính đúng sai của mệnh đề đảo này.
a) Mệnh đề \(P \Rightarrow Q\), phát biểu là: “Nếu a và b chia hết cho c thì a + b chia hết cho c.”
Mệnh đề này đúng nên nó là một định lý.
Giả thiết của định lí: a và b chia hết cho c
Kết luận của định lí: a + b chia hết cho c
Phát biểu định lí dưới dạng điều kiện cần là: “ a + b chia hết cho c là điều kiện cần để có a và b chia hết cho c”
Phát biểu định lí dưới dạng điều kiện đủ là: “ a và b chia hết cho c là điều kiện đủ để có a + b chia hết cho c”
b) Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề \(Q \Rightarrow P\).
Mệnh đề \(Q \Rightarrow P\): “Nếu a + b chia hết cho c thì a và b chia hết cho c”
Mệnh đề này sai.
Chẳng hạn a = 1 và b = 2, c =3. Ta có: \(1 + 2 = 3\; \vdots \;3\), nhưng 1 và 2 không chia hết cho 3.
Phát biểu định lí về hai góc đối đỉnh mọi ng giúp mk vs
Hai góc đối đỉnh là hai góc mà mỗi cạnh là tia đối của một cạnh của góc kia
Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh.
tính chất Hai góc đối đỉnh thì bằng nhau.
1.Phát biểu định lí truyền thẳng của ánh sáng
GIÚP MÌNH NHA BÉ MIN NHÀ CẦN GẤP LẮM
VẬT LÍ
Định luật truyền thẳng của ánh sáng:
_ Trong môi trường trong suốt và đồng tính, ánh sáng truyền đi theo đường thẳng.
Chắc chắn 100%
~ Học tốt ~
trả lời:
Định luật truyền thẳng ánh sáng:
- Trong môi trường trong suốt và đồng tính, ánh sáng truyền đi theo đường thẳng.
Học tốt!
Câu 1: Phát biểu định nghĩa hai góc đối đỉnh (Vẽ hình)
Câu 2: Phát biểu định lí hai góc đối đỉnh
Câu 3: phát biểu định nghĩa hai đường thẳng vuông góc
Câu 4: Phát biểu định nghĩa đường trung trực của đoạn thẳng
Câu 5: Phát biểu dấu hiệu (định lí) nhận bik hai đường thẳng song song
Câu 6: Phát biểu tiên đề ơ clít về đường thẳng song song
Câu 7: Phát biểu tính chất (định lí) của hai đường thẳng song song
Câu 8: Phát biểu định lí về hai đường thẳng phân biệt với một đường thẳng số 3
Câu 9: Phát biểu định lí về hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba
Câu 10: Phát biểu định lí về một đường thẳng vuông góc với một đường thẳng song song
Câu 11: Phát biểu định lí về tổng ba góc của một tam giác
Câu 12: phát biểu tính chất góc ngoài của tam giác, phát biểu ba trường hợp bằng nhau của tam giác
Câu 13: phát biểu các trường hợp bằng nhau của tam giác vuông
(Mọi người ơi mọi người giúp em mấy câu hỏi này với😅Thank you m.n)
vote cho mk xong rồi mk trả lời cho, tin mk đi, mk ko phải n xấu đâu
a) Vẽ c vuông góc với a.
b) Vẽ b// a .Hỏi c có vuông góc với b ko?Vì sao?
c) Phát biểu tính chất đó bằng lời
CÁC BN GIÚP MK BÀI NÀY VS . MK ĐANG CẦN RẤT GẤP SÁNG MAI MK PHẢI ĐI HỌC RỒI.
a _I_ c
a // b
=> b _I_ c
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
Bài này mình đã làm cho bạn ở dưới rồi
a) Vẽ c vuông góc với a.
b) Vẽ b vuông góc với c.Hỏi a có song song với b ko?Vì sao?
c) Phát biểu tính chất đó bằng lời.
CÁC BN GIÚP MK BÀI NÀY VS. MK ĐANG CẦN RẤT GẤP.
a có song song với b.
Gọi giao của a với c là A; của b với c là B
Ta có : \(\widehat{A}=\widehat{B}\left(=90^o\right)\) nên a // b (vì có cặp góc so le trong bằng nhau)
Tính chất : Nếu 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì 2 đường thẳng đó song song với nhau
a) vẽ c ⊥ a.
b ) vẽ b // a
Ta có c ⊥ b vì a // b nên nếu cắt a tại A thì C cũng cắt b tại B. Vì nên
so le trong với nó cũng bẳng 900
Vây c ⊥ b
c) Phát biểu tính chất bằng lời: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
hãy phát biểu định lí diễn tả bởi đầu bài
a//b cvong goc voi a
viết giả thiết kết luận của định lí
Định lý lớn Fermat
Bách khoa toàn thư mở Wikipedia
Đối với các định nghĩa khác, xem Định lý Fermat.

Pierre de Fermat

Phương trình
Định lý cuối của Fermat (hay còn gọi là Định lý lớn Fermat) là một trong những định lý nổi tiếng trong lịch sử toán học. Định lý này phát biểu như sau:
Không tồn tại các nghiệm nguyên khác không x, y, và z thoả mãn xn + yn = zn trong đó n là một số nguyên lớn hơn 2.
Định lý này đã làm khó không biết bao bộ óc vĩ đại của các nhà toán học lừng danh trong gần 4 thế kỉ. Cuối cùng nó được Andrew Wiles chứng minh vào năm 1993 sau gần 8 năm ròng nghiên cứu, phát triển từ chứng minh các giả thiết có liên quan. Tuy nhiên chứng minh này còn thiếu sót và đến năm 1995 Wiles mới hoàn tất, công bố chứng minh trọn vẹn sau 358 năm nỗ lực chứng minh của các nhà toán học. Bằng chứng được mô tả là một 'bước tiến tuyệt vời' trong trích dẫn cho giải thưởng Abel năm 2016. Bằng chứng của Định lý cuối cùng của Fermat cũng đã chứng minh được rất nhiều định lý mô đun và mở ra toàn bộ các phương pháp tiếp cận mới cho nhiều vấn đề khác và kỹ thuật nâng cao tính toán mô đun. Những vấn đề chưa giải quyết đã thúc đẩy sự phát triển của lý thuyết đại số ở thế kỉ 19 và sự chứng minh của định lý Mô- đun ở thế kỉ 20. Đây là định lý trứ danh nhất trong lịch sử toán học. Trước khi chứng minh được nó thì định lý đã được ghi vào sách kỷ lục Guiness thế giới như là một vấn đề toán học khó nhất mọi thời đại, một trong những lý do định lý này được gọi như vậy là vì có một con số khổng lồ các bài chứng minh không thành công.
Tổng quan về định lý[sửa | sửa mã nguồn]
Nguồn gốc của định lý Pytago[sửa | sửa mã nguồn]
Phương trình Pytago, x2 + y2 = z2, có vô số các số nguyên dương cho x, y, z thỏa mãn; các nghiệm này được gọi là bộ ba Pytago. Vào khoảng năm 1637, Fermat đã viết trong một quyển sách rằng phương trình tổng quát hơn là an + bn = cn, không có nghiệm nào là số nguyên dương, nếu n là số nguyên lớn hơn 2. Mặc dù ông tuyên bố có cách chứng minh chung về giả thuyết của ông, Fermat đã không để lại chi tiết về chứng minh của mình, và không có bất kỳ chứng minh nào của ông đã từng được tìm thấy. Khẳng định của ông đã được phát hiện khoảng 30 năm sau cái chết của ông. Tuyên bố này, được gọi là Định lý Cuối cùng của Fermat, đã tồn tại trong toán gần 3,5 thế kỷ. Tuyên bố của Fermat cuối cùng đã trở thành một trong những vấn đề nổi bật nhất chưa được giải quyết của toán học. Những nỗ lực để chứng minh nó đã thúc đẩy sự phát triển đáng kể trong lý thuyết số, và theo thời gian Định lý cuối cùng của Fermat đã nổi bật như là một vấn đề chưa được giải quyết trong toán học.
Sự phát triển và những giải pháp sau đó[sửa | sửa mã nguồn]
Với trường hợp đặc biệt n = 4 do chính Fermat chứng minh, nó đủ để chứng minh định lý cho số mũ là số nguyên tố (sự thu nhỏ chứng minh này được coi là bình thường để chứng minh). Trong hai thế kỷ tiếp theo (1637-1839), phỏng đoán đã được chứng minh chỉ với các số nguyên tố 3, 5 và 7, mặc dù Sophie Germain đã đổi mới và chứng minh một cách tiếp cận có liên quan đến toàn bộ bậc của số nguyên tố. Vào giữa thế kỷ 19, Ernst Kummer đã mở rộng điều này và chứng minh được định lý cho tất cả các số nguyên tố thông thường, để lại các số nguyên tố bất thường được phân tích riêng lẻ. Dựa trên công trình của Kummer và sử dụng các nghiên cứu máy tính phức tạp, các nhà toán học khác có thể mở rộng cách chứng minh để bao gồm tất cả các số nguyên tố chính lên đến bốn triệu, nhưng một bằng chứng cho thấy tất cả các số mũ là không thể tiếp cận được (có nghĩa là các nhà toán học thường xem là một bằng chứng không thể, nó quá khó, không thể chứng minh được với kiến thức hiện tại).
Hoàn toàn tách biệt, khoảng năm 1955, các nhà toán học người Nhật Goro Shimura và Yutaka Taniyama nghi ngờ một liên kết có thể tồn tại giữa các đường cong ellip và dạng mô đun, hai lĩnh vực toán học hoàn toàn khác nhau. Được biết đến vào thời điểm đó là giả thuyết Taniyama-Shimura-Weil, và (cuối cùng) là định lý mô đun, nó tự đứng vững, không có kết nối rõ ràng với Định lý cuối cùng của Fermat. Nó được xem là quan trọng, nhưng nó (như định lý của Fermat) được xem là không thể chứng minh được.
Năm 1984, Gerhard Frey nhận thấy một liên kết rõ ràng giữa hai vấn đề không liên quan và chưa được giải quyết trước đây. Một phác thảo cho thấy điều này có thể được chứng minh đã được đưa ra bởi Frey. Bằng chứng đầy đủ cho thấy hai vấn đề này có liên quan mật thiết với nhau, được xây dựng bởi Ken Ribet vào năm 1986 dựa trên cách chứng minh từng phần của Jean-Pierre Serre, người đã chứng minh được tất cả nhưng chỉ một phần được gọi là "dự đoán epsilon" (xem định lý của Ribet và đường Frey). Bằng tiếng Anh, các giấy tờ của Frey, Serre và Ribet chỉ ra rằng nếu Định lý mô đun có thể được chứng minh cho ít nhất là bán ổn định lớp đường cong ellip, thì một cách chứng minh của Định lý cuối cùng của Fermat cũng sẽ tự động được thực hiện. Kết nối được mô tả dưới đây: bất kỳ giải pháp nào có thể trái ngược với Định lý cuối cùng của Fermat cũng có thể được sử dụng để đảo lại với Định lý mô đun. Vì vậy, nếu định lý Mô-đun đã được tìm thấy là đúng, thì theo định nghĩa không có cách giải nào đảo với Định lý cuối cùng của Fermat có thể tồn tại, điều này cũng phải là đúng.
Mặc dù cả hai vấn đề này đều là những vấn đề khó khăn được xem là "hoàn toàn không thể tiếp cận" được vào thời điểm đó, nhưng đây là gợi ý đầu tiên của một lộ trình mà theo đó Định lý cuối cùng của Fermat có thể được mở rộng và chứng minh cho tất cả các con số, chứ không phải chỉ một số con số. Điều quan trọng là các nhà nghiên cứu lựa chọn một chủ đề nghiên cứu thực sự là không giống như Định lý Cuối cùng của Fermat, Định lý mô đun là một lĩnh vực nghiên cứu chủ yếu mà một cách chứng minh được yêu cầu rộng rãi và không chỉ là một sự kỳ quặc lịch sử, do đó thời gian làm việc trên đó có thể được chứng minh là vo cùng chuyên nghiệp. Tuy nhiên, ý kiến chung cho rằng điều này chỉ đơn giản cho thấy cái không thực tế của chứng minh Taniyama-Shimura phỏng đoán. Phản hồi được trích dẫn từ nhà toán học John Coates:
"Bản thân tôi rất hoài nghi rằng mối liên hệ tuyệt vời giữa Định lý Cuối cùng của Fermat và giả thuyết Taniyama-Shimura sẽ thực sự dẫn đến bất cứ điều gì, bởi vì tôi phải thú nhận rằng tôi không nghĩ rằng giả thuyết Taniyama-Shimura có thể chứng minh được., nó dường như không thể chứng minh. Tôi phải thú nhận rằng tôi nghĩ có lẽ tôi sẽ không chứng kiến điều đó trong suốt cuộc đời mình. "
Khi nghe Ribet đã chứng minh liên kết của Frey là đúng, nhà toán học người Anh Andrew Wiles, người đã có một niềm đam mê từ thời thơ ấu với Định lý cuối cùng của Fermat và có nền tảng làm việc với đường cong ellip và các lĩnh vực liên quan, quyết định thử chứng minh giả thuyết Taniyama-Shimura như một cách để chứng minh Định lý Cuối cùng của Fermat. Năm 1993, sau sáu năm làm việc bí mật về vấn đề này, Wiles đã thành công trong việc chứng minh đủ các giả thuyết để chứng minh Định lý Cuối cùng của Fermat. Bản báo cáo của Wiles có quy mô và phạm vi lớn. Một lỗ hổng đã được phát hiện trong một phần của bài báo gốc của ông trong quá trình xem xét lại và cần thêm một năm nữa và hợp tác với một học sinh cũ, Richard Taylor, để giải quyết. Kết quả là, chứng minh được công bố cuối cùng năm 1995 được kèm theo một báo cáo thứ hai nhỏ hơn cho thấy rằng các bước cố định là hợp lệ. Thành tựu của Wiles được báo cáo rộng rãi trong báo chí nổi tiếng và được phổ biến rộng rãi trong các cuốn sách và chương trình truyền hình. Các phần còn lại của dự đoán Taniyama-Shimura-Weil, bây giờ đã được chứng minh và được gọi là định lý Mô đun, sau đó được chứng minh bởi các nhà toán học khác, người đã xây dựng dựa trên công trình của Wiles từ năm 1996 đến năm 2001. Xứng đáng với chứng minh của ông, Wiles được vinh danh và nhận được nhiều giải thưởng, bao gồm giải thưởng Abel năm 2016.
Các phát biểu tương đương của định lý[sửa | sửa mã nguồn]
Có một số cách khác để tuyên bố định lý cuối cùng của Fermat có toán học tương đương với câu lệnh ban đầu của vấn đề.
Để biểu diễn chúng, chúng ta sử dụng ký hiệu toán học: để N là tập các số tự nhiên 1,2,3,..., để Z là tập các số nguyên 0, ± 1, ± 2,..., và để cho Q là tập các số hợp các số ngẫu nhiên trong đó a và b thuộc Z với b ≠ 0, Dưới đây, chúng ta sẽ gọi một giải pháp cho xn + yn = zn, trong đó một hoặc nhiều x, y, hoặc z có giá trị là 0 thì cách giải sẽ trở nên bình thường. Một giải pháp mà cả ba không phải là giá trị 0 thì sẽ trở nên bất thường.
Để so sánh, chúng ta bắt đầu với công thức ban đầu.
Phát biểu gốc: Với n, x, y, z ∈ N (nghĩa là: x, y, z là tất cả các số nguyên dương) và n> 2 thì phương trình xn + yn = zn vô nghiệm.
Các phương pháp phổ biến nhất của đối tượng theo cách này. Ngược lại, gần như tất cả các sách giáo khoa toán học đều ghi rõ nó qua Z:
Phát biểu tương đương 1[sửa | sửa mã nguồn]
xn + yn = zn, trong đó n ≥ 3, không có các nghiệm bình thường x, y, z ∈ Z.
Tương đương là rõ ràng nếu n là như vậy. Nếu n là lẻ và tất cả ba của x, y, z là âm thì chúng ta có thể thay thế x, y, z bằng -x, -y, -z để có được một cách giải trong N. Nếu hai trong số đó là âm, nó phải là x và z hoặc y và z. Nếu x, z là âm và y là dương, sau đó chúng ta có thể sắp xếp lại để có được (-z) n + yn = (-x) n dẫn đến một cách giải trong N; trường hợp khác được xử lý tương tự. Bây giờ nếu chỉ một trong số chúng là âm, nó phải được x hoặc y. Nếu x là âm, và y và z dương, sau đó nó có thể được sắp xếp lại để lấy (-x) n + zn = yn một lần nữa dẫn đến một cách giải trong N; nếu y là âm, kết quả đối xứng với trước đó. Như vậy trong mọi trường hợp một giải pháp không đối lập trong Z cũng có nghĩa là một giải pháp tồn tại trong N, đó là công thức ban đầu của vấn đề.
Phát biểu tương đương 2[sửa | sửa mã nguồn]
xn + yn = zn, trong đó n ≥ 3, không có các bất thường gì trong cách giải x, y, z ∈ Q.
Điều này là do số mũ của x, y và z bằng nhau (đến n), vì vậy nếu có một cách giải trong Q thì nó có thể được nhân với một mẫu số chung thích hợp để có được một giải pháp trong Z, và do đó kéo theo trong N.
Phát biểu tương đương 3[sửa | sửa mã nguồn]
xn + yn = 1, với n ≥ 3, không có các bất thường gì trong cách giải x, y ∈ Q.
Một giải pháp bất thường a, b, c ∈ Z đến xn + yn = zn cho ra giải pháp khác lạ , ∈ Q cho vn + wn = 1. Ngược lại, một giải pháp một cách giải , ∈ Q to vn + wn = 1 mang lại một gcách giải ad, cb, bd cho xn + yn = zn.
Công thức cuối cùng này đặc biệt hiệu quả, bởi vì nó làm giảm vấn đề từ một vấn đề về bề mặt trong ba chiều với một vấn đề về các đường cong trong hai chiều. Hơn nữa, nó cho phép làm việc trên tập Q, chứ không phải là qua vòng Z; lĩnh vực có cấu trúc nhiều hơnvòng tròn, cho phép phân tích sâu hơn các yếu tố của họ.
Phát biểu tương đương 4[sửa | sửa mã nguồn]
Kết nối với các đường cong ellip: Nếu a, b, c là một giải pháp không tầm thường đối với xp + yp = zp, p là số lẻ, thì y2 = x (x - ap) (x + bp) (đường cong Frey) sẽ là một đường cong ellip.
Xem đường cong ellip này với định lý Ribet cho thấy nó không thể có dạng mô đun. Tuy nhiên, chứng minh của Andrew Wiles chứng minh rằng bất kỳ phương trình có dạng y2 = x (x - an) (x + bn) luôn luôn có một dạng mô đun. Bất kỳ giải pháp nào đối với xp + yp = zp(với p là số lẻ) sẽ tạo ra mâu thuẫn, do đó chứng minh rằng không có các giải pháp nào tồn tại.
(Theo thuật ngữ chung, điều này nói rằng bất kỳ giải pháp nào có thể mâu thuẫn với Định lý cuối cùng của Fermat cũng có thể được sử dụng để mâu thuẫn với Định lý Mô đun.Vì vậy, nếu định lý mô đun được tìm thấy là đúng, thì theo định nghĩa thì không có mâu thuẫn với Định lý cuối cùng của Fermat. Như đã trình bày ở trên, việc khám phá ra tuyên bố tương đương này rất quan trọng đối với giải pháp cuối cùng của Định lý cuối cùng của Fermat, vì nó cung cấp một phương tiện để nó có thể bị 'tấn công' cho tất cả các số cùng một lúc.)
Lịch sử toán học[sửa | sửa mã nguồn]
Pythagoras and Diophantus[sửa | sửa mã nguồn]
Bộ ba số Pytago[sửa | sửa mã nguồn]
Trong thời cổ đại, người ta biết rằng một tam giác có các cạnh lần lượt có tỷ lệ tương ứng là 3: 4: 5 sẽ là một tam giác vuông. Điều này đã được sử dụng trong xây dựng và sau đó sớm được dùng trong hình học. Trong thời cổ đại, điều này đã được phát hiện ra chỉ là một ví dụ của một nguyên tắc chung rằng bất kỳ tam giác nào có tổng bình phương hai cạnh bất kỳ bằng bình phương cạnh còn lại thì tam giác đó là tam giác vuông.
Đây được gọi là định lý Pytago, và một bộ ba số thỏa mãn được điều kiện này được gọi là bộ ba số Pytago. Nó được đặt tên dựa trên tên của nhà toán học Hy Lạp cổ đại- Pytago. Ví dụ các bộ ba (3, 4, 5) và (5, 12, 13). Có rất nhiều bộ ba số như vậy, và các phương pháp để tạo ra bộ ba số đó được nghiên cứu ở nhiều nền văn hóa khác nhau, bắt đầu với người Babylon, sau đó lần lượt là các nhà toán học Hy Lạp, Trung Quốc và Ấn Độ. Về mặt toán học, định nghĩa của một bộ ba số PYtago là một tập gồm ba số nguyên (a, b, c) thỏa mãn phương trình: a2+ b2= c2
Định lý cuối cùng của Fermat xem xét phương trình này cho các giả thiết khác với 2, và cho biết mặc dù có vô số bộ ba thảo mãn phương trình cho n = 2, không có cách giải nào ngoai accsh giải bình thường khi cho x = y = z = 0, tồn tại khi số mũ 2 thay thế bởi bất kỳ số nguyên lớn hơn.
Phương trình Diophantine[sửa | sửa mã nguồn]
Phương trình Fermat, xn + yn = zn với các nghiệm là số nguyên dương, là một ví dụ về phương trình Diophantine, được đặt tên theo tên của nhà toán học Alexandrian ở thế kỷ thứ ba, Diophantus, người đã nghiên cứu chúng và phát triển phương pháp để giải một số phương trình Diophantine. Một vấn đề Diophantine điển hình là tìm hai số nguyên x và y sao cho tổng của chúng và tổng bình phương bằng hai số A và B tương ứng:
A= x+y
B= x2+ y2
Công việc chính của Diophantus là nghiên cứu cuốn Arithmea, nhưng trong đó chỉ còn một vài phần công việc của ông là còn tồn tại. Phỏng đoán của Fermat về Định lý Cuối cùng của ông đã được truyền cảm hứng khi đọc một ấn bản mới của một cuốn sách Arithmea, được Claude Bachet xuất bản và dịch sang tiếng La- tin vào năm 1621.
Phương trình Diophantine đã được nghiên cứu trong hàng ngàn năm. Ví dụ, phương trình Diophantine bậc hai x2 + y2 = z2 được giải bởi các bộ ba số Pytago, ban đầu được giải quyết bởi người Babylon (khoảng 1800 TCN). Cách giải cho các phương trình Diophantine tuyến tính, như 26x + 65y = 13, có thể được tìm thấy bằng thuật toán Euclide (khoảng thế kỷ 5 trước công nguyên). Nhiều phương trình Diophantine có một hình thức tương tự như phương trình của Định lý Cuối cùng của Fermat theo quan điểm của đại số. Ví dụ, có vô số các số nguyên dương x, y, và z sao cho xn + yn = zm trong đó n và m là các số nguyên tố tự nhiên.
Giả thuyết của Fermat[sửa | sửa mã nguồn]
Vấn đề II.8 trong ấn bản 1621 của Arithmea được viết bởi Diophantus. Vì phía bên phải của sách là lề quá nhỏ để chứa cách chứng minh của Fermat về "định lý cuối cùng" của Fermat.
Vấn đề II.8 của Arithmea hỏi làm thế nào một số bình phương nhất định được chia thành hai số bình phương khác; nói cách khác, với một số k nhất định, tìm hai số u và v sao cho k2 = u2 + v2. Diophantus cho thấy làm thế nào để giải quyết vấn đề tổng và bình phương khi k= 4.
Vào khoảng năm 1637, Fermat đã viết bài toán cuối cùng của mình trong bản sao của Arithmea bên cạnh vấn đề tổng bình phương của Diophantus.
Sau cái chết của Fermat năm 1665, con trai của ông, Clément-Samuel Fermat, đã sản xuất một ấn bản mới của cuốn sách (1670) với những nhận xét của cha mình. Mặc dù thời gian đó, nó không hẳn thực sự là một định lý,. Sau này, nó đã được biết đến như Định lý Cuối cùng của Fermat bởi vì nó là tập cuối của các định lý được khẳng định của Fermat mà vẫn không được chứng minh.
Không biết liệu Fermat có thực sự tìm ra cách chứng minh hợp lệ cho tất cả các số mũ n không, nhưng dường như nó là không chắc chắn. Chỉ có một bằng chứng liên quan của ông đã tồn tại, cụ thể là cho trường hợp n = 4, như mô tả trong phần Bằng chứng cho số mũ cụ thể. Trong khi Fermat đặt ra các trường hợp n = 4 và n = 3 như là những thách thức đối với các nhà toán học, như Marin Mersenne, Blaise Pascal, và John Wallis. Ông chưa bao giờ đưa ra một trường hợp chung. Hơn nữa, trong ba mươi năm cuối cùng của cuộc đời, Fermat không bao giờ viết về "cách chứng minh kỳ diệu thực sự" của ông về trường hợp chung, và không bao giờ xuất bản nó. Van der Poorten cho thấy rằng mặc dù sự thiếu xót của một chứng minh là không đáng kể, sự thiếu thách thức có nghĩa là Fermat nhận ra rằng ông không có cách chứng minh nào cả; Trích dẫn Weil thì người ta cho rằng Fermat phải có một thời gian ngắn lừa dối mình với một ý tưởng không thể cứu vãn được nữa.
Các kỹ thuật mà Fermat có thể đã sử dụng trong một "cách chứng minh kỳ diệu" là không được biết đến.
Taylor và chứng minh của Wiles dựa vào các kỹ thuật của thế kỷ 20. Cách chứng minh của Fermat có thể đã được có bản hóa bằng cách so sánh.
Trong khi giả thuyết lớn của Harvey Friedman ngụ ý rằng bất kỳ định lý có thể chứng minh nào (bao gồm định lý cuối cùng của Fermat) có thể được chứng minh bằng cách sử dụng 'số học cơ bản', thì một bằng chứng cần phải là "cơ bản" chỉ theo nghĩa kỹ thuật và có thể liên quan đến hàng triệu bước, quá lâu để có được bằng chứng của Fermat.
Giả thiết Fermat[sửa | sửa mã nguồn]

Bài toán II.8 trong Arithmea của Diophantus, với chú giải của Fermat và sau đó trở thành định lý Fermat cuối cùng (ấn bản 1670)
Định lý này được gọi là định lý cuối cùng của Fermat hay định lý Lớn Fermat là vì vào năm 1630, Fermat cho rằng không thể tìm được nghiệm (nguyên) cho phương trình bậc ba. Điều lý thú ở đây là phỏng đoán này được Fermat viết lại trên lề cuốn sách Arithmea của Diophantus mà không chứng minh, nhưng có kèm theo dòng chữ: “Tôi có một phương pháp rất hay để chứng minh cho trường hợp tổng quát, nhưng không thể viết ra đây vì lề sách quá hẹp." Việc ông có thực sự chứng minh được định lý đó hay không vẫn còn gây tranh cãi, nhưng vấn đề này đã trở thành một vấn đề nổi tiếng trong toán học. Các nhà toán học hết thế hệ này đến thế hệ khác đã cố sức và đều thất bại trong việc tìm ra lời giải cho định lý này.[1]
Với những dòng viết tay đó, nhà toán học người Pháp Pierre de Fermat đã chính thức buông lời thách đố đối với thế hệ các nhà toán học sau ông. Nhiều nhà toán học đã dành cả cuộc đời để cố chứng minh định lý phát biểu nghe có vẻ hết sức đơn giản này.
Hành trình mấy trăm năm để giải lời thách đố, cùng với sự phức tạp của lời giải hàng trăm trang, từ bao thế hệ các nhà toán học đã làm người ta vừa nghi ngờ dòng ghi chú của Fermat, vừa tò mò, thán phục ông.
Lịch sử chứng minh định lý lớn Fermat[sửa | sửa mã nguồn]
Cho tới đầu thế kỷ 20 các nhà toán học chỉ chứng minh định lý này là đúng với n=3, 4, 5, 7 và các bội số của nó. Nhà toán học người Đức Ernst Kummer đã chứng minh định lý này là đúng với mọi số nguyên tố tới 100 (trừ 3 Số nguyên tố phi chính quy là 37, 59, 67).[1]
Nhà toán học vĩ đại người Thụy Sĩ Leonhard Euler (1707 – 1783) đã chứng minh định lý cho trường hợp n=3 và n=4.
Năm 1828, Dirichlet chứng minh cho trường hợp n=5.
Vào những năm 1840, Gabriel Lamé chứng minh với n=7.
200 năm sau Fermat, định lí mới được chứng minh với n=3, 4, 5, 6 và 7.
Định lý quá khó và Bell trong cuốn sách “Bài toán cuối cùng” đã phải viết rằng: có lẽ nền văn minh của chúng ta cáo chung trước khi các nhà toán học tìm ra lời giải cho bài toán.
Tuy vậy, năm 1908, định lý Fermat đột ngột gây được sự chú ý trở lại nhờ công của một nhà công nghiệp và tiến sĩ toán người Đức tên là Paul Wolfshehl. Do gặp phải một chuyện bất hạnh trong đời sống riêng, ông quyết định sẽ tự sát vào lúc nửa đêm. Trong khi chờ đợi, ông tình cờ đọc một chứng minh của Kummer liên quan đến định lí Fermat. Chìm đắm trong sự suy tư, ông vượt qua giờ phút định mệnh lúc nào không biết. Sự đam mê toán học đã hồi sinh cuộc đời ông. Ông quyết định dành gần hết gia sản của mình lập nên giải thưởng Wolfshehl dành tặng cho người nào tìm ra lời giải của định lý Fermat. Trị giá giải thưởng là 100.000 mác tương đương 1,75 triệu USD, lớn hơn giải Nobel.
Khi giải thưởng được thông báo, các bài dự thi ùn ùn đổ về Đại học Gottingen. Ngay trong năm treo giải, có 621 “ lời giải” được đệ trình và mấy năm sau thì số thư từ chất cao đến 3m. Tất cả đều sai.
Quá trình giải của Andrew Wiles[sửa | sửa mã nguồn]
Trong lịch sử công cuộc tìm lời giải cho "Định lý cuối cùng của Fermat" có người phải tự tử và có những người tự lừa chính mình. Cuối cùng sau gần 4 thế kỷ, nhà toán học người Anh, Andrew Wiles cũng công bố lời giải độc nhất vô nhị vào mùa hè năm 1993 và bản chỉnh sửa cuối cùng vào năm 1995, với lời giải dài 200 trang.[1]
Tháng 5 năm 1993, Wiles khoe với vợ của mình là đã giải thành công.Tháng 6 năm 1993, "Ellip Curves and Modular Forms", Wiles lần đầu tiên công bố là ông đã giải được Định lý lớn Fermat.Trong tháng 7 và tháng 8 năm 1993, Nick Katz, đồng nghiệp của Wiles tại Đại học Princeton, trao đổi email với ông về những điểm chưa hiểu rõ, trong đó nhắc rằng trong chứng minh của ông có 1 sai lầm căn bản.Tháng 9 năm 1993, Wiles nhận ra chỗ sai và cố gắng sửa. Trong ngày sinh nhật của vợ ông, ngày 6 tháng 10, bà nói chỉ cần quà sinh nhật là một chứng minh đúng, thế nhưng, dù đã cố gắng hết sức, Wiles vẫn không làm được.Tháng 11 năm 1993, ông gởi email công bố là có trục trặc trong phần của chứng minh đó của mình.Sau nhiều tháng thất bại trong việc tìm hướng giải quyết, Wiles sắp chịu thua. Trong tuyệt vọng, ông yêu cầu giúp đỡ. Richard Taylor, một sinh viên cũ của ông, đã tới Princeton cùng nghiên cứu với ông.
Andrew Wiles
Ba tháng đầu 1994, ông cùng Taylor tìm mọi cách sửa chữa vấn đề nhưng vô hiệu.Tháng 9 năm 1994, ông quay lại nghiên cứu một vấn đề căn bản mà chứng minh của ông được xây dựng dựa trên đó.Ngày 19 tháng 9 năm 1994 phát hiện cách sửa chữa chỗ trục trặc đơn giản và đẹp, dựa trên một cố gắng chứng minh đã làm 3 năm trước. Sau khi coi lại cẩn thận, ông mừng rỡ nói với phu nhân là đã làm được.Tháng 5 năm 1995 đăng lời giải trên Annals of Mathemas (Đại học Princeton).Tháng 8 năm 1995 hội thảo ở Đại học Boston, giới toán học công nhận chứng minh là đúng.Helen G. Grundman, giáo sư toán trường Bryn Mawr College, đánh giá tình hình của cách chứng minh đó như sau:
"Tôi nghĩ là ta có thể nói, vâng, các nhà toán học hiện nay đã bằng lòng với cách chứng minh Định lý lớn Fermat đó. Tuy nhiên, một số sẽ cho là chứng minh đó của một mình Wiles mà thôi. Thật ra chứng minh đó là công trình của nhiều người. Wiles đã có đóng góp đáng kể và là người kết hợp các công trình lại với nhau thành cái mà ông đã nghĩ là một cách chứng minh. Mặc dù cố gắng khởi đầu của ông được phát hiện sau đó là có sai lầm, Wiles và người phụ tá Richard Taylor đã sửa lại được, và nay đó là cái mà ta tin là cách chứng minh đúng Định lý lớn Fermat."
"Chứng minh mà ta biết hiện nay đòi hỏi sự phát triển của cả một lãnh vực toán học chưa được biết tới vào thời Fermat. Bản thân định lý được phát biểu rất dễ dàng và vì vậy xem ra có vẻ đơn giản một cách giả tạo; bạn không cần biết rất nhiều về toán để hiểu bài toán. Tuy nhiên, để rồi nhận ra rằng, theo kiến thức tốt nhất của bạn, cần phải biết rất nhiều về toán mới có thể giải được nó. Vẫn là một câu hỏi chưa có lời đáp rằng liệu có hay không một cách chứng minh Định lý lớn Fermat mà chỉ liên quan tới toán học và các phương pháp đã có vào thời Fermat. Chúng ta không có cách nào trả lời trừ phi ai đó tìm ra một chứng minh như vậy."
Nếu a song song với b mà c vuông góc với c thì b vuông góc với c.
CM nhận định qua đoạn trích Lục Vân Tiên cứu Kiều Nguyệt Nga, Nguyễn Đình Chiểu đã xây dựng 2 nhân vật lí tưởng tiêu biểu cho quan niệm thẩm mỹ của nhân dân.
giúp mk nka m.n
mk cần gấp lém
Cho các định lí:
P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”.
Q: “Nếu \(a < b\) thì \(a + c < b + c\)” (\(a,b,c \in \mathbb{R}\)).
a) Chỉ ra giả thiết và kết luận của mỗi định lí.
b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”.
c) Mệnh đề đảo của mỗi định lí đó có là định lí không?
Tham khảo:
a)
Mệnh đề P có dạng \(R \Rightarrow T\)với R: “Hai tam giác bằng nhau” và T: “Diện tích của hai tam giác bằng nhau”
Giả thiết là mệnh đề R: “Hai tam giác bằng nhau”
Kết luận là mệnh đề T: “Diện tích của hai tam giác bằng nhau”
Mệnh đề Q có dạng \(A \Rightarrow B\)với A: “\(a < b\)” và B: “\(a + c < b + c\)”
Giả thiết là mệnh đề A: “\(a < b\)”
Kết luận là mệnh đề B: “\(a + c < b + c\)”
b)
+) Mệnh đề P có thể phát biểu lại như sau:
Hai tam giác bằng nhau là điều kiện đủ để có diện tích của chúng bằng nhau.
Diện tích của hai tam giác bằng nhau là điều kiện cần để hai tam giác bằng nhau.
+) Mệnh đề Q có thể phát biểu lại như sau:
\(a < b\) là điều kiện đủ để có \(a + c < b + c\).
\(a + c < b + c\)là điều kiện cần để có \(a < b\).
c)
Mệnh đề đảo của mệnh đề P có dạng \(T \Rightarrow R\), phát biểu là: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau”.
Mệnh đề này sai nên không là định lí.
Chẳng hạn: Tam giác ABC và tam giác DEF, có diện tích bằng nhau nhưng hai tam giác không bằng nhau.
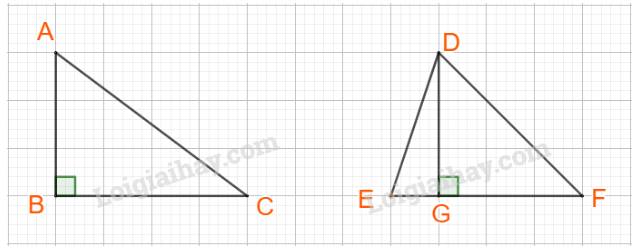
Mệnh đề đảo của mệnh đề Q có dạng \(B \Rightarrow A\), phát biểu là: “Nếu \(a + c < b + c\)thì \(a < b\)”.
Mệnh đề này đúng nên nó cũng là định lí.
Muốn chia các căn bậc hai của số a không âm cho căn bậc hai của số b dương ta có thể chia a cho cho b rồi khai phương kết quả đó