Trên cạnh Ox , Oy của góc xOy lấy 2 điểm Avaf B / OA = OB tia pg của xOy cắt AB ở C và C là trung điểm của AB. CMR AB vuông góc với OC

Những câu hỏi liên quan
Trên hai cạnh Ox và Oy của góc xOy , lấy hai điểm A và B sao cho OA=OB , tia phân giác của Oz của góc xOy cắt AB tại C a) CMR C là trung điểm của AB và Oz vuông góc với AB b) trên tia Cz lấy điểm M sao cho OC=CM CMR AM//OB và BM//OA C) kẻ MI vuông gốc với Ox , MK vuông góc với Oy so sánh BI và AK
I don't now
or no I don't
..................
sorry
Đúng 0
Bình luận (0)
Trên hai cạnh Ox và Oy của góc xOy , lấy hai điểm A và B sao cho OA=OB , tia phân giác của Oz của góc xOy cắt AB tại C a) CMR C là trung điểm của AB và Oz vuông góc với AB b) trên tia Cz lấy điểm M sao cho OC=CM CMR AM//OB và BM//OA C) kẻ MI vuông gốc với Ox , MK vuông góc với Oy so sánh BI và AK
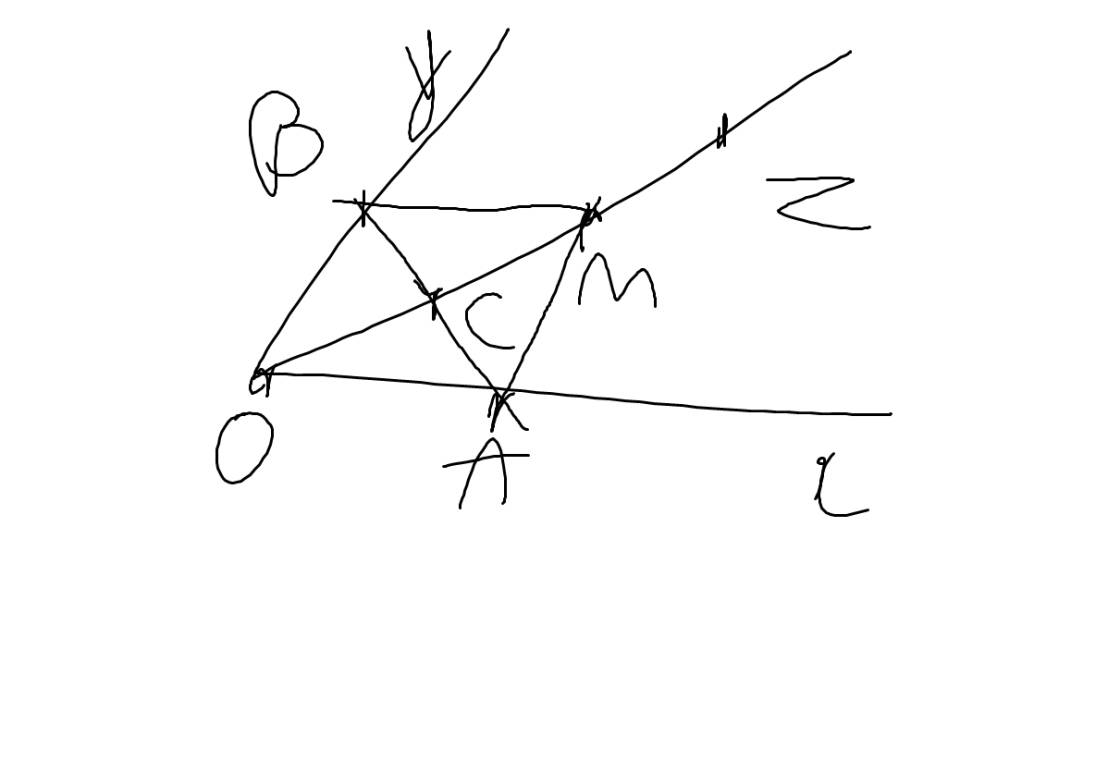
Trên hai cạnh Ox và Oy của xOy lấy hai điểm A và B sao cho OA = OB, tia phân giác Oz của góc xOy cắt AB tại C a) CMR: C là trung điểm của AB và Oc ⊥ AB b) Trên tia Cz lấy điểm M sao cho OC = CM.Chứng minh: AM//OB và BM//OA c) Kẻ MI ⊥ Oy, MK ⊥ Ox. So sánh BI và AK d) Goi N la giao diem cua AI va BK, c/m O,N,M thang hang
Trên cạnh Ox và Oy của góc xOy lấy hai điểm A và B sao cho OA = Ob, tia phân giác Oz của góc xOy ắt AB tại C.
a) CMR: C là trung điểm của ab và AC vuông góc với OC
b) Trên tia Cz lấy điểm M sao cho OC = Cm. CMR AM//OB, BM//OA
Vẽ hình giúp em ạ
a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>AC=BC
=>C là trung điểm của AB
Ta có: CA=CB
=>C nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
=>CO\(\perp\)AB
b: Xét ΔOAC và ΔMBC có
CO=CM
\(\widehat{OCA}=\widehat{MCB}=90^0\)
CA=CB
Do đó: ΔOAC=ΔMBC
=>\(\widehat{OAC}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên OA//BM
Xét ΔCBO vuông tại C và ΔCAM vuông tại C có
CB=CA
CO=CM
Do đó: ΔCBO=ΔCAM
=>\(\widehat{CBO}=\widehat{CAM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BO//AM
Đúng 2
Bình luận (0)
Trên các cạnh Ox, Oy của góc xOy, lấy các điểm A và B sao cho OA=OB. Tia phân giác của góc xOy cắt AB ở C. Chứng minh rằng
a) C là trung điểm của AB
b) AB vuông góc với OC
cho góc xoy lấy điểm a trên tia ox điểm b trên tia oy sao cho oa=ob tia phân giac xoy cắt ab ở c chứng minh: c là trung điểm của ab; ab vuông góc với oc
trên cạnh ox và oy của góc xOy lấy điểm a và b sao cho oa= ob , tia phân giác Oz của góc xOy cắt AB tại c
a chứng minh rằng c là trung điểm của ab và ac vuông góc với oc
b trên tia cz lấy điểm m sao cho oc=cm .chứng minh am//ob,bm//oa
c kẻ mi vuông góc với oy ,mk vuông góc với ox. so sánh bi và ak ( vẽ hình và ghi gt / kl)
a: ΔOAB cân tại O
mà OC là phân giác
nên OC vuông góc AB và C là trung điểm của AB
b: Xét tứ giác OAMB có
C là trung điểm chung của OM và AB
=>OAMB là hình bình hành
=>OA//MB và OB//MA
Đúng 0
Bình luận (0)
Trên các cạnh Ox và Oy của góc xOy, lấy các điểm A và B sao cho OA= OB. Tia phân giác của góc xOy cắt AB ở C.
a) chứng minh ∆AOC = ∆BOC
b) chứng minh AB vuông góc với OC
c) lấy điểm D trên tia OC sao cho C là trung điểm của OD. Chứng minh AD song song với OB
Trên các cạnh Ox và Oy của góc xOy, lấy các điểm A và B sao cho OA = OB. Tia phân giác của góc xOy cắt AB ở C. CMR : C là trung điểm của AB.
Xét tam giác OAC và tam giác OAB
OA = OB
OC chung
Góc AOC = góc OAB
=> Tam giác OAC = tam giác OAB
=> AC = AB
=> C là trung điểm của AB.
Đúng 0
Bình luận (0)
có OA=OB
suy ra tam giác AOB cân tại O
xét tam giác OAC và tam giác OBC có
OA=OB
AOC=BOC
OC chung
suy ra tam giác AOC=tam giác BOC
suy ra CA=BC(tương ứng)
mà C nằm giữa A,B
suy ra C là trung điểm của AB
Đúng 0
Bình luận (0)
Làm thử :
Xét \(\Delta OAC\) và \(\Delta OBC\) có :
\(AB=AC\) \(\left(GT\right)\)
\(\widehat{AOC}=\widehat{BOC}\) ( vì OC là tia phân giác của góc xOy )
OC là cạnh chung
Do đó : \(\Delta OAC=\Delta OBC\) \(\left(c-g-c\right)\)
Suy ra : \(AC=BC\) ( hai cạnh tương ứng )
\(\Rightarrow\)\(C\) là trung điểm của \(AB\)
Vậy \(C\) là trung điểm của \(AB\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời














