Cho các số a,b,c thoả mãn \(a+b+c+ab+bc+ca=36\)chứng minh rằng \(a^2+b^2+c^2\ge27\)

Những câu hỏi liên quan
Cho các số dương \(a,b,c\) thoả mãn \(a+b+c=3\). Chứng minh rằng: \(\dfrac{a^2+bc}{b+ca}+\dfrac{b^2+ca}{c+ab}+\dfrac{c^2+ab}{a+bc}\ge3\)
Cho các số a, b, c thỏa mãn a + b + c + ab + bc + ac = 36. Chứng minh rằng \(a^2+b^2+c^2\ge27\)
Lời giải:
Áp dụng BĐT AM-GM ta có:
$a^2+9\geq 2\sqrt{9a^2}=2|3a|\geq 6a$
Tương tự: $b^2+9\geq 6b; c^2+9\geq 6c$
Cộng theo vế:
$a^2+b^2+c^2\geq 6(a+b+c)-27(*)$
Cũng áp dụng BĐT AM-GM:
$a^2+b^2\geq 2\sqrt{a^2b^2}=2|ab|\geq 2ab$
Hoàn toàn tương tự và cộng theo vế:
$2(a^2+b^2+c^2)\geq 2(ab+bc+ac)$
$\Leftrightarrow 6(a^2+b^2+c^2)\geq 6(ab+bc+ac)(**)$
Lấy $(*)+(**)\Rightarrow 7(a^2+b^2+c^2)\geq 6(a+b+c+ab+bc+ac)-27=6.36-27=189$
$\Rightarrow a^2+b^2+c^2\geq 27$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=3$
Đúng 0
Bình luận (0)
Cho `a,b,c` là các số dương thoả mãn điều kiện `a+b+c+ab+bc+ca=6`
Chứng minh rằng : \(\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge a^2+b^2+c^2\ge3\)
Áp dụng bất đẳng thức Cô si cho hai số dương ta có:
(a2 + b2) + (b2 + c2) + (c2 + a2) ≥ 2ab + 2bc + 2ca
=> 2(a2 + b2 + c2 ) ≥ 2 (ab + bc + ca) (1) (a2 + 1) + (b2 + c2) + (c2 + a2) ≥ 2a + 2b + 2c
=> a2 + b2 + c2 + 3 ≥ 2(a + b + c) (2)
Cộng các vế của (1) và (2) ta có:
3 ( a2 + b2 + c2 ) + 3 ≥ 2 (ab + bc + ca + a + b + c)
=> 3( a2 + b2 + c2 ) + 3 ≥ 12 => a2 + b2 + c2 ≥ 3.
Ta có: (a^3/b + ab ) + ( b^3/c + bc ) + ( c^3/a + ca)≥ 2(a2 + b2 + c2) (CÔ SI)
<=>a^3/b + b^3/c + c^3/a +ab + bc + ac ≥ 2(a2 + b2 + c2)
Vì a2 + b2 + c2 ≥ ab + bc + ca => a^3 + b^3 + c^3 ≥ a2 + b2 + c2 ≥ 3 (đpcm).
Đúng 0
Bình luận (0)
Áp dụng bất đẳng thức cô-si cho hai số dương ta có:
\(\left(a^2+b^2\right)+\left(b^2+c^2\right)+\left(c^2+a^2\right)\ge2ab+2bc+2ca\)
\(\Rightarrow2\left(a^2+b^2+c^2\right)\ge2\left(ab+bc+ca\right)\) (1)
\(\left(a^2+b^2\right)+\left(b^2+c^2\right)+\left(c^2+a^2\right)\ge2a+2b+2c\)
\(\Rightarrow a^2+b^2+c^2+3\ge2\left(a+b+c\right)\) (2)
Cộng (1) với (2)
\(3\left(a^2+b^2+c^2\right)+3\ge2\left(ab+bc+ca+a+b+c\right)\)
\(\Rightarrow3\left(a^2+b^2+c^2\right)+3\ge12\)
\(\Rightarrow a^2+b^2+c^2\ge3\)
Ta có: \(\left(\dfrac{a^3}{b}+ab\right)+\left(\dfrac{b^3}{c}+bc\right)+\left(\dfrac{c^3}{a}+ca\right)\ge2\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}+ab+bc+ca\ge2\left(a^2+b^2+c^2\right)\)
Vì \(a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge a^2+b^2+c^2\ge3\) (đpcm).
Đúng 0
Bình luận (0)
Xét BĐT phụ: `a^2+b^2+c^2>=ab+bc+ca(**)`
`BĐT(**)<=>1/2[(a-b)^2+(b-c)^2+(c-a)^2]>=0AAa;b;c` xảy ra dấu "=" khi `a=b=c`
Từ `BĐT(**)` cộng hai vế với `2(ab+bc+ca)` ta có `(a+b+c)^2>=3(ab+bc+ca)<=>(a+b+c)^2/3>=ab+bc+ca`
-----
Ta có `6=a+b+c+ab+bc+ca<=a+b+c+(a+b+c)^2/3=t^2/3+t(t=a+b+c>0)`
`=>t^2/3+t-6>=0=>t>=3` hay `a+b+c>=3`
Áp dụng BĐT Cauchy-Schwarz ta có:
`a^3/b+b^3/c+c^3/a=a^4/(a)+b^4/(bc)+c^4/ca>=(a^2+b^2+c^2)/(ab+bc+ca)>=a^2+b^2+c^2>=(a+b+c)^2/3=3`
Đúng 0
Bình luận (0)
Cho ba số thực dương a, b, c thoả mãn a+b+c=2 Chứng minh rằng:
\(\dfrac{ab}{\sqrt{2c+ab}}+\dfrac{bc}{\sqrt{2a+bc}}+\dfrac{ca}{\sqrt{2b+ca}}\le1\)
\(VT=\sqrt{\dfrac{a^2b^2}{c\left(a+b+c\right)+ab}}+\sqrt{\dfrac{b^2c^2}{a\left(a+b+c\right)+bc}}+\sqrt{\dfrac{a^2c^2}{b\left(a+b+c\right)+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{ac+ab+bc+c^2}}+\sqrt{\dfrac{b^2c^2}{a^2+ac+ab+bc}}+\sqrt{\dfrac{a^2c^2}{ab+bc+b^2+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{\left(c+a\right)\left(b+c\right)}}+\sqrt{\dfrac{a^2c^2}{\left(b+c\right)\left(a+b\right)}}+\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\)
Áp dụng BĐT Cauchy-Schwarz:
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\le\dfrac{\dfrac{bc}{a+b}+\dfrac{bc}{a+c}}{2}\\\sqrt{\dfrac{a^2c^2}{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\dfrac{ca}{a+b}+\dfrac{ca}{b+c}}{2}\\\sqrt{\dfrac{a^2b^2}{\left(b+c\right)\left(a+c\right)}}\le\dfrac{\dfrac{ab}{b+c}+\dfrac{ab}{a+c}}{2}\end{matrix}\right.\)
\(\Rightarrow VT\le\dfrac{\left(\dfrac{bc}{a+b}+\dfrac{ca}{a+b}\right)+\left(\dfrac{ca}{b+c}+\dfrac{ab}{b+c}\right)+\left(\dfrac{bc}{a+c}+\dfrac{ab}{a+c}\right)}{2}\\ \Rightarrow VT\le\dfrac{a+b+c}{2}=\dfrac{2}{2}=1\)
Dấu \("="\Leftrightarrow a=b=c=\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
Cho a,b,c thỏa mãn :ab+bc+ca=9. Chứng minh rằng: \(a^4+b^4+c^4\ge27\)
Cho a,b,c là các số thực dương thoả mãn \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\le3\)Chứng minh rằng \(\dfrac{a}{1+b^2}+\dfrac{b}{1+c^2}+\dfrac{c}{1+a^2}+\dfrac{1}{2}\left(ab+bc+ca\right)\ge3\)
Đặt\(P=\dfrac{a}{1+b^2}+\dfrac{b}{1+c^2}+\dfrac{c}{1+a^2+}+\dfrac{1}{2}\left(ab+bc+ca\right)\)
Bổ đề: \(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge9\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{9}{a+b+c}\) (1)
Chứng minh bổ đề: \(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge9\sqrt[3]{abc.\dfrac{1}{abc}}=9\left(\forall a,b,c\ge0\right)\)
Kết hợp điều kiện đề bài ta được: \(a+b+c\ge3\)
Ta có: \(\dfrac{ab^2}{1+b^2}\le\dfrac{ab^2}{2\sqrt{b^2}}=\dfrac{ab}{2}\) ( AM-GM cho 2 số không âm 1 và b^2 )
\(\Rightarrow\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab}{2}\left(1\right)\)
Chứng minh hoàn toàn tương tự: \(\dfrac{b}{1+c^2}\ge b-\dfrac{bc}{2}\left(2\right)\)
\(\dfrac{c}{1+a^2}\ge c-\dfrac{ca}{2}\left(3\right)\)
Cộng (1),(2),(3) vế theo vế thu được: \(P\ge a+b+c=3\)
Dấu "=" xảy ra tại a=b=c=1
Đúng 7
Bình luận (0)
Cho a, b, c là các số thực dương thoả mãn a+b+c=3. Chứng minh rằng:
\(\frac{a}{b^2\left(ca+1\right)}+\frac{b}{c^2\left(ab+1\right)}+\frac{c}{a^2\left(bc+1\right)}\ge\frac{9}{\left(1+abc\right)\left(ab+bc+ca\right)}\)
Theo bđt Cauchy - Schwart ta có:
\(\text{Σ}cyc\frac{c}{a^2\left(bc+1\right)}=\text{Σ}cyc\frac{\frac{1}{a^2}}{b+\frac{1}{c}}\ge\frac{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+a+b+c}\)\(=\frac{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+3}\)
\(=\frac{\left(ab+bc+ca\right)^2}{abc\left(ab+bc+ca\right)+3a^2b^2c^2}\)
Đặt \(ab+bc+ca=x;abc=y\).
Ta có: \(\frac{x^2}{xy+3y^2}\ge\frac{9}{x\left(1+y\right)}\Leftrightarrow x^3+x^3y\ge9xy+27y^2\)
\(\Leftrightarrow x\left(x^2-9y\right)+y\left(x^3-27y\right)\ge0\) ( luôn đúng )
Vậy BĐT đc CM. Dấu '=' xảy ra <=> a=b=c=1
làm sao mà \(x\left(x^2-9y\right)+y\left(x^3-27y\right)\ge0\)lại luôn đúng
Cho a, b, c là các số dương thoả mãn: a+b+c=1. Chứng minh bất đẳng thức: \(\sqrt{ab+c}\) + \(\sqrt{bc+a}\) + \(\sqrt{ca+b}\) ≤ 2
Lời giải:
Áp dụng BĐT AM-GM:
$\text{VT}=\sqrt{ab+c(a+b+c)}+\sqrt{bc+a(a+b+c)}+\sqrt{ca+b(a+b+c)}$
$=\sqrt{(c+a)(c+b)}+\sqrt{(a+b)(a+c)}+\sqrt{(b+a)(b+c)}$
$\leq \frac{c+a+c+b}{2}+\frac{a+b+a+c}{2}+\frac{b+a+b+c}{2}$
$=2(a+b+c)=2$
Ta có đpcm.
Dấu "=" xảy ra khi $a=b=c=\frac{1}{3}$
Đúng 0
Bình luận (0)
cho a,b,c là 3 số dương thoả mãn 1/a + 1b + 1/c <=3 .chứng minh rằng a/(1+b^2) + b/(1+c^2) + c/(1+a^2) + 1/2(ab+bc+ca) >= 3













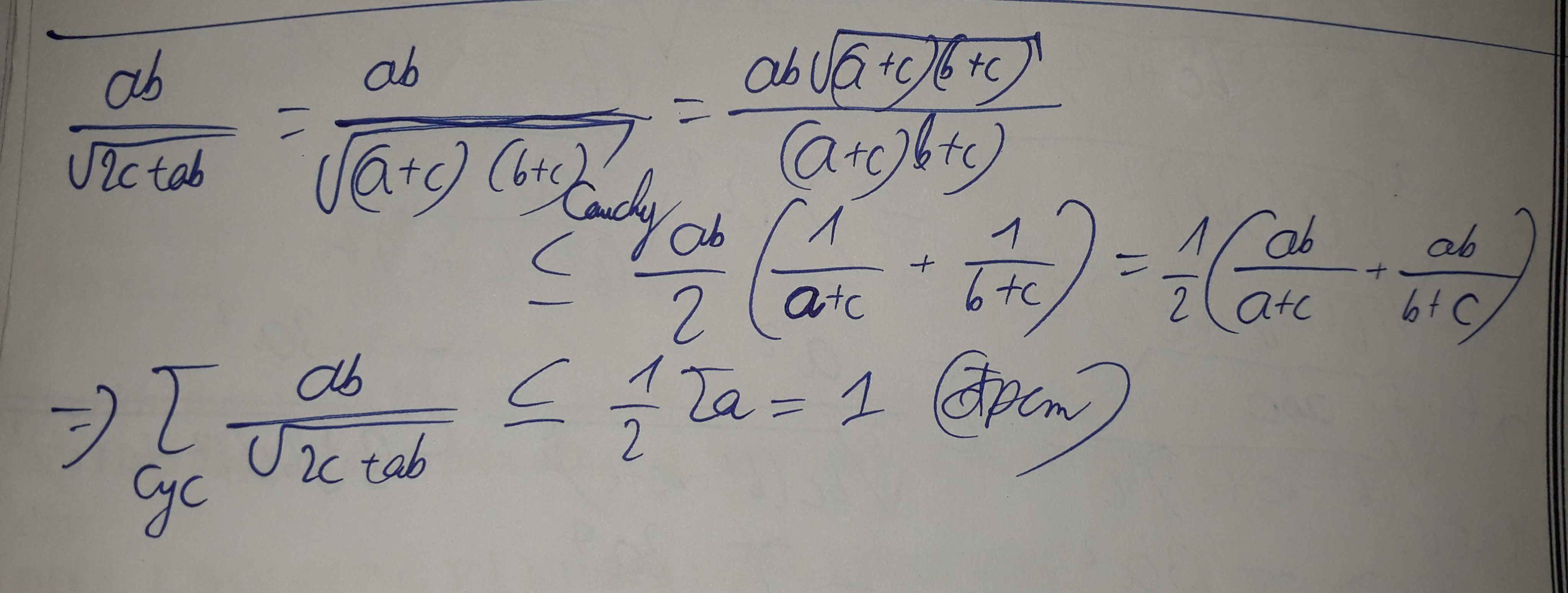





 iải của
iải của


