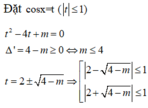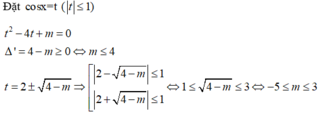tìm m để phương trình \(\frac{3sinx+m}{4cosx-3}\)=2 có nghiệm

Những câu hỏi liên quan
Tìm điều kiện của m để phương trình
3
sin
x
+
4
cos
x
m
có nghiệm.
Đọc tiếp
Tìm điều kiện của m để phương trình 3 sin x + 4 cos x = m có nghiệm.
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có đồ thị như hình bên dưới.Có bao nhiêu giá trị nguyên của tham số m để phương trình f(3sinx + 4cosx) f(m) có nghiệm? A. 10 B. 14. C. 9 D. 11.
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình bên dưới.
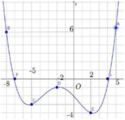
Có bao nhiêu giá trị nguyên của tham số m để phương trình f(3sinx + 4cosx) = f(m) có nghiệm?
A. 10
B. 14.
C. 9
D. 11.
Tìm m để các bất phương trình sau đúng với mọi x: (3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1 A. m 1 B. m 1 C. m 2 D. m ≤ 0
Đọc tiếp
Tìm m để các bất phương trình sau đúng với mọi x:
(3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1
A. m = 1
B. m > 1
C. m > 2
D. m ≤ 0
Đáp án D
Đặt t = 3sin x - 4cos x => -5 ≤ t ≤ 5 (dùng bất đẳng thức bunhiacopxki)
Ta có: y = (3sin x – 4cos x)2 – 6sin x + 8cos x
= t2 – 2t = (t – 2)2 -1
Do -5 ≤ t ≤ 5 => 0 ≤ (t – 2)2 ≤ 36 => min y = -1
Suy ra yêu cầu bài toán -1 ≥ 2m - 1 ⇔ m ≤ 0.
Đúng 0
Bình luận (0)
Tìm m để các bất phương trình
(
3
sin
x
-
4
cos
x
)
2
-
6
sin
x
+
8
cos
x
≥
2
m
-
1
đúng với mọi
x
∈
ℝ
A. m 0 B.
m
≤
0...
Đọc tiếp
Tìm m để các bất phương trình ( 3 sin x - 4 cos x ) 2 - 6 sin x + 8 cos x ≥ 2 m - 1 đúng với mọi x ∈ ℝ
A. m> 0
B. m ≤ 0
C. m < 0
D. m ≤ 1
Xét hàm số y= ( 3sinx – 4cosx )2 – 6sinx + 8cosx
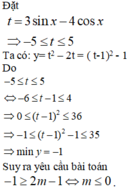
Đáp án B
Đúng 0
Bình luận (0)
tìm m để bất pt \(\left(3sinx-4cosx\right)^2-6sinx+8cosx\ge2m-1\) có nghiệm đúng với mọi x thuộc R
đặt \(3sinx-4cosx=t\) đk \(-5\le t\le5\) pt trên trở thành \(t^2-2t\ge2m-1\)
\(\left(t-1\right)^2\ge2m\Leftrightarrow m\le0\)
Đúng 0
Bình luận (2)
Cho hàm số yf(x) liên tục trên
ℝ
và có bảng biến thiên như hình dưới đâySố các số nguyên m thỏa mãn phương trình
f
(
3
sin
x
+
4
cos
x
+
5
)
m
có nghiệm là A. 10001 B. 20000 C. 20001 D. 10000
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có bảng biến thiên như hình dưới đây
Số các số nguyên m thỏa mãn phương trình f ( 3 sin x + 4 cos x + 5 ) = m có nghiệm là

A. 10001
B. 20000
C. 20001
D. 10000
Tìm điều kiện của tham số m để phương trình
cos
2
x
-4cosx+m0 có nghiệm. A. m4 B.-5 m 3 C.
m
≤
4
D. -5
≤
m
≤
3
Đọc tiếp
Tìm điều kiện của tham số m để phương trình cos 2 x -4cosx+m=0 có nghiệm.
A. m<4
B.-5< m < 3
C. m ≤ 4
D. -5 ≤ m ≤ 3
Tìm điều kiện của tham số m để phương trình
cos
2
x
-
4
cos
x
+
m
0
có nghiệm A. m 4 B. -5 m 3 C.
m
≤
4
D.
-
5
≤
m
≤
3
Đọc tiếp
Tìm điều kiện của tham số m để phương trình cos 2 x - 4 cos x + m = 0 có nghiệm
A. m< 4
B. -5 <m< 3
C. m ≤ 4
D. - 5 ≤ m ≤ 3
Tìm điều kiện của tham số m để phương trình
cos
2
x
−
4
cos
x
+
m
0
có nghiệm A. m 4 B. -5 m 3 C.
m
≤
4.
D. ...
Đọc tiếp
Tìm điều kiện của tham số m để phương trình cos 2 x − 4 cos x + m = 0 có nghiệm
A. m < 4
B. -5 < m < 3
C. m ≤ 4.
D. − 5 ≤ m ≤ 3.
Đáp án D
t 2 − 4 t + m = 0 Δ ' = 4 − m ≥ 0 ⇔ m ≤ 4 t = 2 ± 4 − m ⇒ 2 − 4 − m ≤ 1 2 + 4 − m ≤ 1 ⇔ 1 ≤ 4 − m ≤ 3 ⇔ − 5 ≤ m ≤ 3
Đúng 0
Bình luận (0)