- Nếu m = 5 thì A ∩ B = 151;

- Nếu m < 5 thì A ∩ B = Ø;

- Nếu m > 5 thì A ∩ B = [5; m];

Chúc bạn học tốt ~

- Nếu m = 5 thì A ∩ B = 151;

- Nếu m < 5 thì A ∩ B = Ø;

- Nếu m > 5 thì A ∩ B = [5; m];

Chúc bạn học tốt ~

- Nếu m = 5 thì A ∩ B = 151;

- Nếu m < 5 thì A ∩ B = Ø;

- Nếu m > 5 thì A ∩ B = [5; m];

Chúc bạn học tốt ~ 

= a ( tk mk nha )

a co co tan cung la

0;1;2;3;4;5;6;7;8;9

từ 0 đến 9

thể nào cx đúng!!!

m<0 nên m<1/3m

\(\Leftrightarrow\left(-\infty;m\right)\cap\left(\dfrac{1}{3m};+\infty\right)=\varnothing\)

Gọi cạnh tam giác là a thì \(a=R\sqrt{3}\)

Do tính đối xứng của đường tròn và tam giác đều, không mất tính tổng quát, giả sử M nằm trên cung nhỏ BC

\(\Rightarrow\widehat{BMC}=180^0-\widehat{BAC}=120^0\)

\(\Rightarrow AM.BC=AB.CM+AC.BM\Leftrightarrow AM=BM+CM\)

\(\Rightarrow S=\left(BM+CM\right)^2+2BM^2-3CM^2\)

\(=3BM^2+2BM.CM-2CM^2\)

Lại có: \(BC^2=BM^2+CM^2-2MB.MC.cos\widehat{BMC}\)

\(=BM^2+CM^2+MB.MC\Rightarrow MB.MC=3R^2-BM^2-CM^2\)

\(\Rightarrow S=6R^2+BM^2-4CM^2\)

Gọi I là điểm thỏa mãn \(\overrightarrow{BI}-4\overrightarrow{CI}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BI}=\dfrac{4}{3}\overrightarrow{BC}\)

\(\Rightarrow BI=\dfrac{4\sqrt{3}}{3}R\) ; \(CI=\dfrac{\sqrt{3}}{3}R\)

\(S=6R^2+\left(\overrightarrow{BI}+\overrightarrow{IM}\right)^2-4\left(\overrightarrow{CI}+\overrightarrow{IM}\right)^2\)

\(S=6R^2+BI^2-4CI^2-3IM^2=10R^2-3IM^2\)

\(S_{max}\) khi \(IM_{min}\Rightarrow M\equiv C\Rightarrow S=CA^2+2CB^2=9R^2\)

Hmm, sao lại không có nhỉ, thử cách khác.

O đồng thời là trọng tâm tam giác

\(S=\left(\overrightarrow{MO}+\overrightarrow{OA}\right)^2+2\left(\overrightarrow{MO}+\overrightarrow{OB}\right)^2-3\left(\overrightarrow{MO}+\overrightarrow{OC}\right)^2\)

\(=OA^2+2OB^2-3OC^2+2\overrightarrow{MO}\left(\overrightarrow{OA}+2\overrightarrow{OB}-3\overrightarrow{OC}\right)\)

\(=2\overrightarrow{MO}\left[\overrightarrow{CO}+\overrightarrow{OA}+2\overrightarrow{CO}+2\overrightarrow{OB}\right]\)

\(=2\overrightarrow{MO}\left(\overrightarrow{CA}+2\overrightarrow{CB}\right)=2\overrightarrow{MO}.\overrightarrow{CE}\)

Với E là điểm sao cho \(\overrightarrow{CA}+2\overrightarrow{CB}=\overrightarrow{CE}\)

Ta có: \(AE=CD=2BC=2\sqrt{3}R\) ; \(\widehat{CAE}=120^0\)

\(\Rightarrow CE=\sqrt{AC^2+AE^2-2AC.AE.cos120^0}=R\sqrt{21}\)

\(S=2\overrightarrow{MO}.\overrightarrow{CE}=2MO.CE.cos\left(\widehat{MO};\overrightarrow{CE}\right)=2R.R\sqrt{21}.cos\left(\overrightarrow{MO};\overrightarrow{CE}\right)\)

\(=2\sqrt{21}R^2.cos\left(\overrightarrow{MO};\overrightarrow{CE}\right)\le2\sqrt{21}R^2\)

\(\Rightarrow S_{max}=2\sqrt{21}R^2\) khi \(\overrightarrow{OM}\) cùng chiều \(\overrightarrow{CE}\)

Lần này chắc là đúng rồi, sai sót của bài làm cũ ở chỗ biểu thức S không đối xứng A; B; C nên việc giả sử M nằm trên cung nhỏ BC là sai 

Update thêm cái hình vẽ cho bạn dễ hình dung

a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.

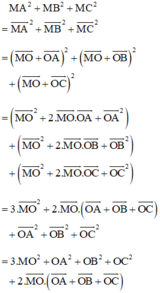
Lại có:

+ O là trọng tâm tam giác nên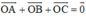 

+ Bán kính đường tròn ngoại tiếp tam giác:

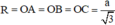
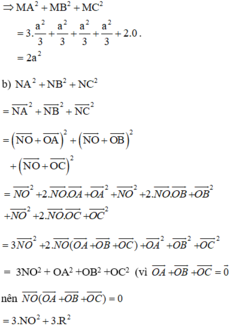
Ta có: NA2 + NB2 + NC2 ngắn nhất

⇔ NO2 ngắn nhất vì R không đổi

⇔ NO ngắn nhất

⇔ N là hình chiếu của O trên d.

Where do you live?
-> I live in Ho Chi Minh City.
What can you do there?
-> I can travel across the city by bus or motorbike.
Do you like it? Why/Why not?
-> Yes, I do like it. Because I can visit many places such as Duc Ba Cathedral....

Bạn tham khảo nha

I live in Binh Thuan province

I can go swimming, go supermarket, hang out with my friends,....

Yes, i do. Because this place is convenient, the air is fresh and cool

C

B. Các nguyên tố tham gia

( Bạn có thể xem trong SGK- Công nghệ 8 trang 61 )

- Dựa vào tỉ lệ cacbon và các nguyên tố tham gia, người ta chia kim loại đen thành 2 loại chính là gang và thép.