a)    Ta có:

\(\begin{array}{l}{\sin ^4}\alpha  - {\cos ^4}\alpha  = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow \left( {{{\sin }^2}\alpha  + {{\cos }^2}\alpha } \right)\left( {{{\sin }^2}\alpha  - {{\cos }^2}\alpha } \right) = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow {\sin ^2}\alpha  - {\cos ^2}\alpha  - 1 + 2{\cos ^2}\alpha  = 0\\ \Leftrightarrow {\sin ^2}\alpha  + {\cos ^2}\alpha  - 1 = 0\\ \Leftrightarrow 1 - 1 = 0\\ \Leftrightarrow 0 = 0\end{array}\)

Đẳng thức luôn đúng

b)    Ta có:

\(\begin{array}{l}\tan \alpha  + \cot \alpha  = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{\cos \alpha .\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{1}{{\sin \alpha .\cos \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\end{array}\)

Đẳng thức luôn đúng

vế trái =\(\frac{\sin}{1+\cot}\)+\(\frac{\cos}{1+\tan}\)= \(\frac{sin}{1+\frac{cos}{sin}}\)+\(\frac{cos}{1+\frac{sin}{cos}}\)= \(\frac{sin^2}{\sin+cos}\)+\(\frac{cos^2}{sin+cos}\)= \(\frac{sin^2+cos^2}{sin+cos}\)=\(\frac{1}{sin+cos}\)= vế phải

https://vietjack.com/giai-toan-lop-9/bai-14-trang-77-sgk-toan-9-tap-1.jsp

bạn tham khảo ở đây nhé

giả sử: ta có, ABC vuông tại A, góc an-pha là góc B

\(sin\alpha=sinB=\frac{CA}{CB}\)

\(cos\alpha=cosB=\frac{AB}{BC}\)

\(tan\alpha=tanB=\frac{CA}{AB}\)

\(cot\alpha=cotB=\frac{AB}{CA}\)

do đó,

a) \(\frac{sin\alpha}{cos\alpha}=\frac{sinB}{cosB}=\frac{\frac{CA}{BC}}{\frac{AB}{BC}}=\frac{CA}{BC}.\frac{BC}{AB}=\frac{CA}{AB}=tan\alpha\)

b) câu b thì cậu giải tương tự như câu a vậy

\(a=\left(\frac{sina+\frac{sina}{cosa}}{cosa+1}\right)^2+1=\left(\frac{sina\left(cosa+1\right)}{cosa\left(cosa+1\right)}\right)^2+1\)

\(=tan^2a+1=\frac{1}{cos^2a}\)

\(b=\frac{sina}{cosa}\left(\frac{1+cos^2a-sin^2a}{sina}\right)=\frac{sina}{cosa}\left(\frac{2cos^2a}{sina}\right)=2cosa\)

\(c=1-\frac{cos^2a}{cot^2a}+\frac{sina.cosa}{\frac{cosa}{sina}}=1-cos^2a.\frac{sin^2a}{cos^2a}+\frac{sin^2a.cosa}{cosa}\)

\(=1-sin^2a+sin^2a=1\)

\(1+tan^2a=1+\frac{sin^2a}{cos^2a}=\frac{cos^2a+sin^2a}{cos^2a}=\frac{1}{cos^2a}\)

\(1+cot^2a=1+\frac{cos^2a}{sin^2a}=\frac{sin^2a+cos^2a}{sin^2a}=\frac{1}{sin^2a}\)

\(cot^2a-cos^2a=\frac{cos^2a}{sin^2a}-cos^2a=cos^2a\left(\frac{1}{sin^2a}-1\right)=cos^2a\left(\frac{1-sin^2a}{sin^2a}\right)\)

\(=cos^2a.\frac{cos^2a}{sin^2a}=cos^2a.cot^2a\)

Câu cuối đề bài sai

Tham khảo:

a) 

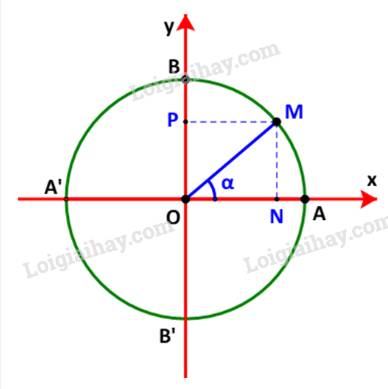
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha  = {x^2}\\{\sin ^2}\alpha  = {y^2}\end{array} \right.\)(1)

Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)

Từ (1) và (2) suy ra \({\sin ^2}\alpha  + {\cos ^2}\alpha  = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)

\( \Rightarrow {\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) (vì OM =1). (đpcm)

b) 

Ta có:  \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha  \ne {90^o})\)

\( \Rightarrow 1 + {\tan ^2}\alpha  = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\)

Mà theo ý a) ta có \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) với mọi góc \(\alpha \)

\( \Rightarrow 1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm)

c) 

Ta có:  \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha  < {180^o})\)

\( \Rightarrow 1 + {\cot ^2}\alpha  = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\)

Mà theo ý a) ta có \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) với mọi góc \(\alpha \)

\( \Rightarrow 1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)