Cho góc xOy. Điểm A thuộc Ox ; B thuộc Oy. Qua A vẽ đường thẳng a vuông góc với Ox ; qua B vẽ đường thẳng b vuông góc với Oy. CMR :
a) Nếu a cắt b thì xOy < 180o
b) Nếu a // b thì xOy = 180o
c) Nếu a | b thì xOy = 90o
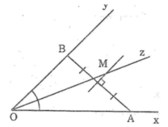
Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy. Hãy tìm điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy); cách đều Ox, Oy và cách đều A, B.
Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.
Bài 2: Cho góc nhọn xOy. Gọi I là một điểm thuộc tia phân giác của góc xOy. Kẻ IA vuông góc với Ox (điểm A thuộc tia Ox) và IB vuông góc với Oy (điểm B thuộc tia Oy) a) Chứng minh △OAI = △OBI, IA = IB.
b) Cho biết OI = 10cm, AI = 6cm. Tính OA.
c) Gọi K là giao điểm của BI và Ox và M là giao điểm của AI với Oy. So sánh AK và BM?
d) Gọi C là giao điểm của OI và MK. Chứng minh OC vuông góc với MK
a: Xét ΔOAI vuông tại A và ΔOBI vuông tại B có
OI chung
\(\widehat{AOI}=\widehat{BOI}\)
Do đó: ΔOAI=ΔOBI
Suy ra: IA=IB
b: \(OA=\sqrt{OI^2-AI^2}=8\left(cm\right)\)
c: Xét ΔAIK vuông tại A và ΔBIM vuông tại B có
IA=IB
\(\widehat{AIK}=\widehat{BIM}\)
Do đó: ΔAIK=ΔBIM
Suy ra: AK=BM
Cho góc nhọn xOy. Gọi I là một điểm thuộc tia phân giác của góc xOy. Kẻ IA vuông góc với Ox (điểm A thuộc tia Ox) và IB vuông góc với Oy (điểm B thuộc tia Oy)
a, Chứng minh IA = IB. b, Cho biết OI = 10cm, AI = 6cm. Tính OA.
c, Gọi K là giao điểm của BI và Ox và M là giao điểm của AI với Oy. So sánh AK và BM?
d, Gọi C là giao điểm của OI và MK. Chứng minh OC vuông góc với MK.
mình xin cả hình vẽ nhé ![]()
Câu 5:Cho góc nhọn xOy. Gọi I là một điểm thuộc tia phân giác của góc xOy. Kẻ IA vuông góc với Ox (điểm A thuộc tia Ox) và IB vuông góc với Oy (điểm B thuộc tia Oy)
a) Chứng minh IA = IB.
b) Cho biết OI = 10cm, AI = 6cm. Tính OA.
c) Gọi K là giao điểm của BI và Ox và M là giao điểm của AI với Oy. So sánh AK và BM?
d) Gọi C là giao điểm của OI và MK. Chứng minh OC vuông góc với MK.
a: Xét ΔOAI vuông tại A và ΔOBI vuông tại B có
OI chung
\(\widehat{AOI}=\widehat{BOI}\)
Do đó: ΔOAI=ΔOBI
Suy ra: IA=IB
b: \(OA=\sqrt{OI^2-IA^2}=8\left(cm\right)\)
c: Xét ΔIAK vuông tại A và ΔIBM vuông tại B có
IA=IB
\(\widehat{AIK}=\widehat{BIM}\)
Do đó: ΔIAK=ΔIBM
Suy ra: AK=BM
Cho góc xOy khác góc bẹt. Oz là tia phân giác của góc xOy. A là điểm nằm trong góc xOz. Vẽ BA ⊥\vuông góc Ox (B thuộc Ox), AC vuông góc Oy (C thuộc Oy). Chứng minh rằng AB < AC.
Cho góc xOy = 100o. Lấy điểm A bên trong xOy. Qua A kẻ AH vuông góc Ox và AK vuông góc với Oy (H thuộc Ox ; K thuộc Oy). Khi đó góc KAH = ... o?
Nối AO.
Xét tam giác HAO vuông tại H:
Góc HAO + Góc AOH = 90 độ
Xét tam giác AOK vuông tại K:
Góc KAO + góc KOA =90 độ
=> Góc HAO + Góc AOH + Góc KAO + góc KOA =180 độ
(Góc HAO+ Góc KAO)+( Góc AOH +góc KOA)=180 độ
Góc KAH + Góc HOK =180 độ
Góc KAH + 100 độ =180 độ
=> Góc KAH = 80 độ
cậu vẽ hình ra đi mk lười vẽ mk bị bệnh
góc đó =80 độ nhé@@!
Ta có góc xOy+AKO+AHO+HAK=360
mà xOy=100
AKO=90
AHO=90
=> HAK=360-90-90-100=80 độ nhé!
Cho góc xOy= 100 độ. Lấy điểm A trong góc xOy. Qua A kẻ AHvuông góc vs Ox, AK vuông góc vs Oy ( H thộc Ox, K thuộc Oy). Tính HAK???
góc HAK là:
360độ-góc AHO-góc AKO- góc HOK=gócHAK
góc HAK=360 độ-90 độ- 90 độ- 100 độ=80 độ
vậy HAK=80 độ
k nha, please
Góc HAK là:
3600 - góc AHO - góc AKO - góc HOK = góc HAK
Góc HAK = 3600 - 900 - 900 - 1000 = 800
Vậy HAK = 800
Cho góc xOy vuông. Lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy, điểm C thuộc A và B. Gọi Ox' là tia đối của tia Ox. Hãy vẽ hình.
Cho góc xOy có số đo bằng 120o , điểm A thuộc tia phân giác của góc xOy . Kẻ AB vuông góc với Ox (B thuộc Ox), kẻ Ax vuông góc với Oy (C thuộc Oy), tam giác ABC là tam giác gì ? Vì sao ?
Ta có: OA là tia phân giác của \(\widehat{xOy}\)(gt)
nên \(\widehat{xOA}=\widehat{yOA}=\dfrac{\widehat{xOy}}{2}=\dfrac{120^0}{2}=60^0\)
hay \(\left\{{}\begin{matrix}\widehat{BOA}=60^0\\\widehat{COA}=60^0\end{matrix}\right.\)
Ta có: ΔAOC vuông tại C(AC\(\perp\)Oy tại C)
nên \(\widehat{CAO}+\widehat{COA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{CAO}=30^0\)
Ta có: ΔAOB vuông tại B(AB\(\perp Ox\) tại B)
nên \(\widehat{BAO}+\widehat{BOA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BAO}=30^0\)
Ta có: \(\widehat{CAB}=\widehat{CAO}+\widehat{BAO}\)(tia AO nằm giữa hai tia AB,AC)
\(\Leftrightarrow\widehat{CAB}=30^0+30^0\)
hay \(\widehat{CAB}=60^0\)
Xét ΔAOC vuông tại C và ΔAOB vuông tại B có
AO chung
\(\widehat{CAO}=\widehat{BAO}\left(=30^0\right)\)
Do đó: ΔAOC=ΔAOB(cạnh huyền-góc nhọn)
hay AC=AB(hai cạnh tương ứng)
Xét ΔABC có AB=AC(cmt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)(cmt)
nên ΔABC đều(Dấu hiệu nhận biết tam giác đều)
Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy
a) Hãy tìm điểm M nằm trong góc xOy, cách đều Ox, Oy và cách đều A, B
b) Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a) ?
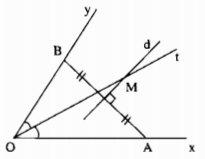
a) - Điểm nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên nó thuộc tia phân giác Ot của góc xOy
- Điểm cách đều 2 điểm A và B thuộc đường thẳng d là đường trung trực của AB
Vậy M là giao điểm của dường trung trực của đoạn thẳng AB và tia phân giác Ot của góc xOy
b) Nếu OA = OB
⇒ ∆OAB cân tại O
Tia phân giác của góc xOy cũng là đường trung trực của AB. Vậy bất kỳ điểm M nào nằm trên tia phân giác của góc xOy đều thỏa mãn điều kiện câu a.