a: Ta có: ΔAHB vuông tại H

mà HP là đường trung tuyến

nên HP=AP

hay P nằm trên đường trung trực của AH(1)

Ta có: ΔAHC vuông tại H 

mà HN là đường trung tuyến

nên HN=AN

hay N nằm trên đường trung trực của AH(2)

Từ (1) và (2) suy ra PN là đường trung trực của AH

Lời giải:

$M,N$ lần lượt là trung điểm $AB, AC$ nên $MN$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$

$\Rightarrow MN\parallel BC$ hay $MN\parallel HP$

$\Rightarrow MNPH$ là hình thang $(*)$

Mặt khác:
Tam giác vuông $ABH$ có $HM$ là đường trung tuyến ứng với cạnh huyền nên $HM=\frac{AB}{2}=MB$ (bổ đề quen thuộc)

$\Rightarrow $MHB$ cân tại $M$

$\Rightarrow \widehat{MHB}=\widehat{MBH}$

Mà $\widehat{MBH}=\widehat{NPC}$ (hai góc đồng vị với $NP\parallel AB$)

$\Rightarrow \widehat{MHB}=\widehat{NPC}$

$\Rightarrow 180^0-\widehat{MHB}=180^0-\widehat{NPC}$

Hay $\widehat{MHP}=\widehat{NPH}(**)$

Từ $(*); (**)\Rightarrow $MNPH$ là hình thang cân (đpcm)

Hình vẽ: 

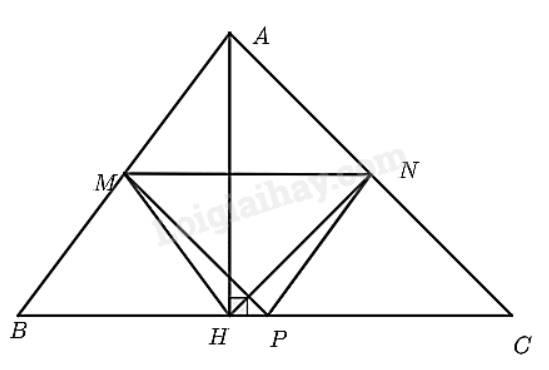
- Vì \(M\) là trung điểm của \(AB;N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\). Do đó, \(MN//BC\) (tính chất đường trung bình).

\( \Rightarrow MN//HP\left( {H;P \in BC} \right)\)

Xét tứ giác \(MNPH\) có: \(MN//HP \Rightarrow \) tứ giác \(MNPH\) là hình thang.

- Vì \(M\) là trung điểm của \(AB;P\) là trung điểm của \(AC\) nên \(MP\) là đường trung bình của tam giác \(ABC\). Do đó, \(MP = \frac{1}{2}AC\) (tính chất đường trung bình) (1).

- Xét tam giác \(AHC\) vuông tại \(H\) có:

\(N\)là trung điểm của \(AC\) nên \(HN = \frac{1}{2}AC\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (2).

Từ (1) và (2) suy ra \(MP = HN\).

Xét hình thang \(MNPH\) có: \(MP = HN\) (chứng minh trên).

Do đó, hình thang \(MNPH\) là hình thang cân (dấu hiệu nhận biết hình thang cân).

a: Xét ΔABC có

M là trung điểm của AB

N là trung điểm của AC

Do đó:MN là đường trung bình của ΔBAC

Suy ra: MN//BC

Xét ΔABH có 

M là trung điểm của AB

MI//BH

Do đó:I là trung điểm của AH

a: Xét ΔABC có 

M là trung điểm của AB

N là trung điểm của AC

Do đó: MN là đường trung bình

=>MN//BC

Xét tứ giác BDNC có 

DN//BC

BD//NC

Do đó: BDNC là hình bình hành

b: Xét tứ giác BDNH có BH//DN

nên BDNH là hình thang

câu c mik có cm tương tự trong trang mình á vô coi cho nhanh==''

a: Xét ΔABC có

M là trung điểm của AB

N là trung điểm của AC

Do đó: MN là đường trung bình của ΔBAC

Suy ra: MN//BC

Xét ΔABH có

M là trung điểm của AB

MI//BH

Do đó: I là trung điểm của AH

cutsgrrrrrrrrrrrcccc5gcbvj4545651253

1) Vì I là trung điểm của AB ; K là trung điểm của AC => IK là đường trung bình của Tam giác ABC

=> IK // BC hay tứ giác IKCB là hình thang

2) Vì I là trung điểm của AB ; N  là trung điểm của BH => IN là đường trung bình của tam giác ABH 

=> IN = \(\frac{1}{2}\) AH (1)

Vì K là trung điểm của AC ; M là trung điểm của HC => KM là đường trung bình của tam giác ACH

=> KM = \(\frac{1}{2}\) AH

Từ (1); (2) => \(IN=KM=\frac{1}{2}AH\)