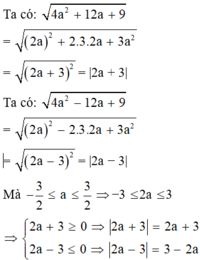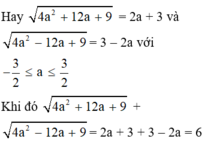Đáp án đúng : A

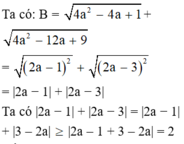
Dấu “=” xảy ra  ⇔ 2 a − 1 3 − 2 a ≥ 0 ⇔ 1 2 ≤ a ≤ 3 2

Vậy GTNN của B là 2 khi  1 2 ≤ a ≤ 3 2

\(A=\left|m+1\right|+\left|m-4\right|=\left|m+1\right|+\left|4-m\right|>=\left|m+1+4-m\right|=5\)

Dấu = xảy ra khi -1<=m<=4

Đáp án đúng : C

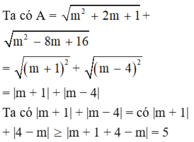
Dấu “=” xảy ra  ⇔ m + 1 4 − m ≥ 0

⇔ − 1 ≤ m ≤ 4

Vậy GTNN của A là 5 khi  − 1 ≤ m ≤ 4

Lời giải:

$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$

$=(2a+b)^2-6(2a+b)+3b^2-6b+12$

$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$

$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$

Vậy $P_{\min}=0$

Giá trị này đạt tại $2a+b-3=b-1=0$

$\Rightarrow b=1; a=1$

Lời giải:

$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$

$=(2a+b)^2-6(2a+b)+3b^2-6b+12$

$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$

$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$

Vậy $P_{\min}=0$

Giá trị này đạt tại $2a+b-3=b-1=0$

$\Rightarrow b=1; a=1$

bài này sử dụng định lí vi-ét nha

Đáp án đúng : D

PT x 2 − 2 m + 1 x + m 2 − 1 = 0     ( 1 ) có 2 nghiệm phân biệt x 1 , x 2

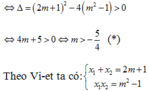
Theo Vi-et ta có:  x 1 + x 2 = 2 m + 1 x 1 x 2 = m 2 − 1

Ta có:  x 1 2 + x 2 2 + 8 x 1 x 2 = x 1 + x 2 2 + 6 x 1 x 2 = 2 m + 1 2 + 6 m 2 − 1

= 10 m 2 + 2 5 m + 1 25 − 27 5 = 10 m + 1 5 2 − 27 5

⇒ x 1 2 + x 2 2 + 8 x 1 x 2 ≥ − 27 5

Dấu ‘=’ xảy ra khi m = − 1 5 (thỏa mãn (*))

Vậy x 1 2 + x 2 2 + 8 x 1 x 2 đạt giá trị nhỏ nhất khi  m = − 1 5

Đáp án cần chọn là: C

A=|m+1|+|m-1|=|m+1|+|1-m|>=|m+1+1-m|=2

Dấu = xảy ra khi -1<=m<=1

B=|2a-1|+|2a-3|=|2a-1|+|3-2a|>=|2a-1+3-2a|=2

Dấu = xảy ra khi 1/2<=a<=3/2

a) Xét pt đã cho có \(a=m^2+m+1\); \(b=-\left(m^2+2m+2\right)\); \(c=-1\)

Nhận thấy rằng \(ac=\left(m^2+m+1\right)\left(-1\right)=-\left(m^2+m+1\right)\)

\(=-\left(m^2+2m.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)=-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\)

Vì \(-\left(m+\dfrac{1}{2}\right)^2\le0\) và \(-\dfrac{3}{4}< 0\) nên \(-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}< 0\) hay \(ac< 0\). Vậy pt đã cho luôn có 2 nghiệm trái dấu.

b) Theo câu a, ta đã chứng minh được pt đã cho luôn có 2 nghiệm trái dấu \(x_1,x_2\).

Áp dụng hệ thức Vi-ét, ta có \(S=x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m^2+2m+2\right)}{m^2+m+1}=\dfrac{m^2+2m+2}{m^2+m+1}\)

Nhận thấy \(m^2+m+1\ne0\) nên ta có:

\(\left(m^2+m+1\right)S=m^2+2m+2\) \(\Leftrightarrow Sm^2+Sm+S-m^2-2m-2=0\)\(\Leftrightarrow\left(S-1\right)m^2+\left(S-2\right)m+\left(S-2\right)=0\)(*)

pt (*) có \(\Delta=\left(S-2\right)^2-4\left(S-1\right)\left(S-2\right)\)\(=S^2-4S+4-4\left(S^2-3S+2\right)\)\(=S^2-4S+4-4S^2+12S-8\)\(=-3S^2+8S-4\)

Để pt (*) có nghiệm thì \(\Delta\ge0\) hay \(-3S^2+8S-4\ge0\)\(\Leftrightarrow-3S^2+6S+2S-4\ge0\)\(\Leftrightarrow-3S\left(S-2\right)+2\left(S-2\right)\ge0\) \(\Leftrightarrow\left(S-2\right)\left(2-3S\right)\ge0\)

Ta xét 2 trường hợp:

TH1: \(\left\{{}\begin{matrix}S-2\ge0\\2-3S\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\ge2\\S\le\dfrac{2}{3}\end{matrix}\right.\)

TH2: \(\left\{{}\begin{matrix}S-2\le0\\2-3S\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\le2\\S\ge\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\dfrac{2}{3}\le S\le2\) (nhận)

Khi \(S=\dfrac{2}{3}\) thì (*) \(\Leftrightarrow\left(\dfrac{2}{3}-1\right)m^2+\left(\dfrac{2}{3}-2\right)m+\dfrac{2}{3}-2=0\)\(\Leftrightarrow-\dfrac{1}{3}m^2-\dfrac{4}{3}m-\dfrac{4}{3}=0\)\(\Leftrightarrow m^2+4m+4=0\)

\(\Leftrightarrow\left(m+2\right)^2=0\) \(\Leftrightarrow m+2=0\) \(\Leftrightarrow m=-2\)

Khi \(S=2\) thì (*) \(\Leftrightarrow\left(2-1\right)m^2+\left(2-2\right)m+2-2=0\)\(\Leftrightarrow m^2=0\)

  \(\Leftrightarrow m=0\)

Vậy GTNN của S là \(\dfrac{2}{3}\) khi \(m=-2\) và GTLN của S là \(2\) khi \(m=0\)