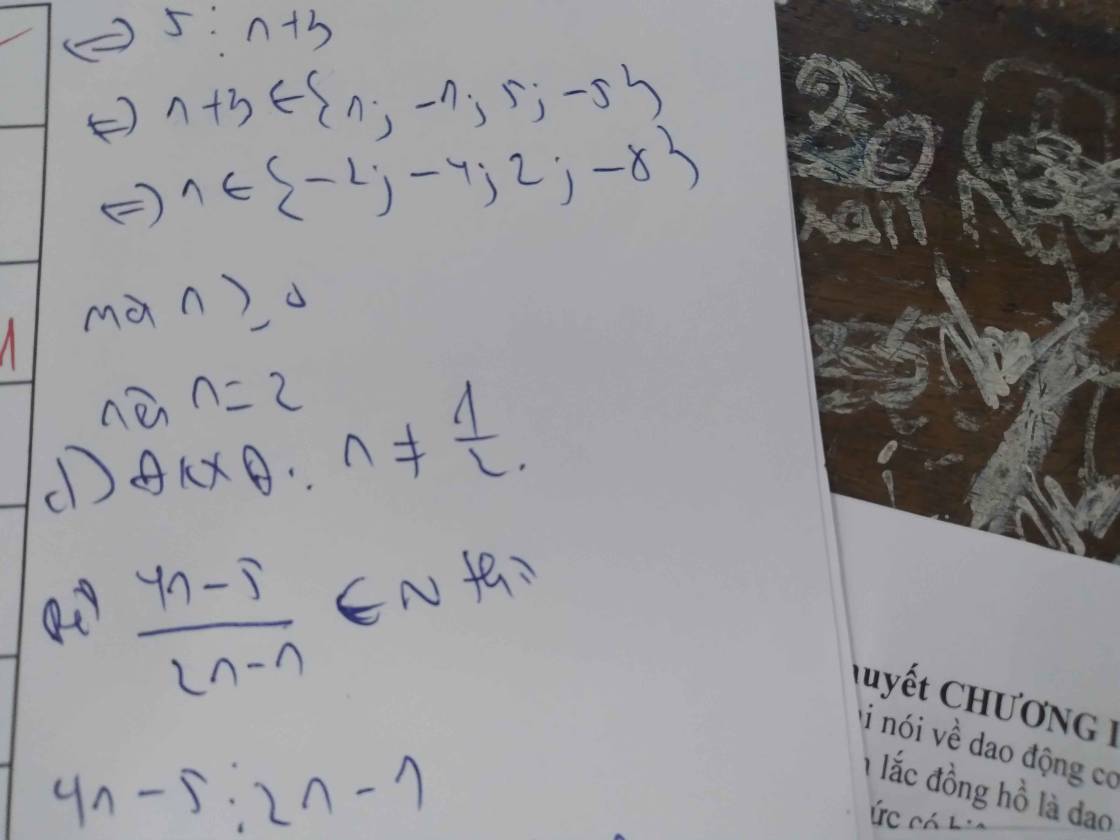Tìm n thuộc N để n^2+4n là số CP

Những câu hỏi liên quan
tìm n thuộc để n2+ 4n + 3 là số chính phương với mọi n thuộc N
Cho A=n3-4n2+4n-1.Tìm n thuộc N để A là số nguyên tố
Bài 1: Cho A = n+10/2n+8
a) TÌm n thuộc Z để A là phân số
b) Tìm n thuộc Z để A thuộc Z
Bài 2: TÌm n thuộc Z để 2n+3/4n+1 là phân số tối giản
Tìm n thuộc Z để các số sau cp
a,n^2-n+13
b,n+18 và n-41 đều cp
Giúp mình mấy bài này nha
bài 1 : Tìm n thuộc N để phân số 2n-1/3n+2 có giá trị là số nguyên dương
Bài 2: Tìm n thuộc N để phân số n+3/4n-1 có giá trị là số nguyên âm
Bài 3: Tìm n thuộc N để phân số 2n+5/3n+1 có giá trị là số tự nhiên
2.Tìm n thuộc N. Để các phân số sau có giá trị là số tự nhiên.
a,15/n b,7/n-2 c,n+8/n+3 d,4n-5/2n-1
1. Cho phân số A= 8n +193 / 4n + 3
a, Tìm n thuộc N để A là số tự nhiên
b, Tìm n thuộc N để A là phân số tối giản
tìm n thuộc Z để các số sau là số nguyên:
a.6n-4/2n+1
b.3n+2/4n-4
c.4n-1/3-2n
`a in ZZ`
`=>6n-4 vdots 2n+1`
`=>3(2n+1)-7 vdots 2n+1`
`=>7 vdots 2n+1`
`=>2n+1 in Ư(7)={+-1,+-7}`
`=>2n in {0,-2,6,-8}`
`=>n in {0,-1,3,-4}`
`b in ZZ`
`=>3n+2 vdots 4n-4`
`=>12n+8 vdots 4n-4`
`=>3(4n-4)+20 vdots 4n-4`
`=>20 vdots 4n-4`
`=>4n-4 in Ư(20)={+-1,+-2,+-4,+-5,+-10,+-20}`
`=>4n-4 in {+-4,+-20}`
`=>n-1 in {+-1,+-5}`
`=>n in {0,2,6,-4}`
`c in ZZ`
`=>4n-1 vdots 3-2n`
`=>2(3-2n)-7 vdots 3-2n`
`=>7 vdots 3-2n`
`=>3-2n in Ư(7)={+-1,+-7}`
`=>2n in {4,0,-4,10}`
`=>n in {2,0,-2,5}`
Đúng 2
Bình luận (2)
a) đk: \(n\ne\dfrac{-1}{2}\)
Để \(\dfrac{6n-4}{2n+1}\) nguyên
<=> \(\dfrac{3\left(2n+1\right)-7}{2n+1}\) nguyên
<=> \(3-\dfrac{7}{2n+1}\) nguyên
<=> \(7⋮2n+1\)
Ta có bảng
| 2n+1 | 1 | -1 | 7 | -7 |
| n | 0 | -1 | 3 | -4 |
| tm | tm | tm | tm |
b)đk: \(n\ne1\)
Để \(\dfrac{3n+2}{4n-4}\) nguyên
=> \(\dfrac{3n+2}{n-1}\) nguyên
<=> \(\dfrac{3\left(n-1\right)+5}{n-1}\) nguyên
<=> \(3+\dfrac{5}{n-1}\) nguyên
<=> \(5⋮n-1\)
Ta có bảng:
| n-1 | 1 | -1 | 5 | -5 |
| n | 2 | 0 | 6 | -4 |
| Thử lại | tm | loại | tm | loại |
c) đk: \(n\ne\dfrac{3}{2}\)
Để \(\dfrac{4n-1}{3-2n}\) nguyên
<=> \(\dfrac{4n-1}{2n-3}\) nguyên
<=> \(\dfrac{2\left(2n-3\right)+5}{2n-3}\) nguyên
<=> \(2+\dfrac{5}{2n-3}\) nguyên
<=> \(5⋮2n-3\)
Ta có bảng:
| 2n-3 | 1 | -1 | 5 | -5 |
| n | 2 | 1 | 4 | -1 |
| tm | tm | tm | tm |
Đúng 0
Bình luận (0)
Giải:
a) \(\dfrac{6n-4}{2n+1}\)
Để \(\dfrac{6n-4}{2n+1}\) là số nguyên thì \(6n-4⋮2n+1\)
\(6n-4⋮2n+1\)
\(\Rightarrow6n+3-7⋮2n+1\)
\(\Rightarrow7⋮2n+1\)
\(\Rightarrow2n+1\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
Ta có bảng giá trị:
| 2n+1 | -7 | -1 | 1 | 7 |
| n | -4 | -1 | 0 | 3 |
Vậy \(n\in\left\{-4;-1;0;3\right\}\)
b) \(\dfrac{3n+2}{4n-4}\)
Để \(\dfrac{3n+2}{4n-4}\) là số nguyên thì \(3n+2⋮4n-4\)
\(3n+2⋮4n-4\)
\(\Rightarrow12n+8⋮4n-4\)
\(\Rightarrow12n-12+20⋮4n-4\)
\(\Rightarrow20⋮4n-4\)
\(\Rightarrow4n-4\inƯ\left(20\right)=\left\{\pm1;\pm2;\pm4;\pm5;\pm10;\pm20\right\}\)
Ta có bảng giá trị:
| 4n-4 | -20 | -10 | -5 | -4 | -2 | -1 | 1 | 2 | 4 | 5 | 10 | 20 |
| n | -4 (t/m) | \(\dfrac{-3}{2}\) (loại) | \(\dfrac{-1}{4}\) (loại) | 0 (t/m) | \(\dfrac{1}{2}\) (loại) | \(\dfrac{3}{4}\) (loại) | \(\dfrac{5}{4}\) (loại) | \(\dfrac{3}{2}\) (loại) | 2 (t/m) | \(\dfrac{9}{4}\) (loại) | \(\dfrac{7}{2}\) (loại) | 6 (t/m) |
Vậy \(n\in\left\{-4;0;2;6\right\}\)
c) \(\dfrac{4n-1}{3-2n}\)
Để \(\dfrac{4n-1}{3-2n}\) là số nguyên thì \(4n-1⋮3-2n\)
\(4n-1⋮3-2n\)
\(\Rightarrow6-4n+1⋮3-2n\)
\(\Rightarrow1⋮3-2n\)
\(\Rightarrow3-2n\inƯ\left(1\right)=\left\{\pm1\right\}\)
Ta có bảng giá trị:
| 3-2n | -1 | 1 |
| n | 2 | 1 |
Vậy \(n\in\left\{1;2\right\}\)
Chúc bạn học tốt!
Đúng 0
Bình luận (0)
tìm n thuộc z để số hữu tỉ 4n^2-9/2n+3 là số nguyên
\(\dfrac{4n^2-9}{2n+3}=\dfrac{\left(2n+3\right)\left(2n-3\right)}{2n+3}=2n-3\)
Để \(\dfrac{4n^2-9}{2n+3}\) là số nguyên
\(\Rightarrow2n-3\in Z\)
\(\Rightarrow\forall n\in Z\)
Đúng 2
Bình luận (0)