Gọi C là vị trí của máy bay

Gọi CH là độ cao của máy bay so với mặt đất

=>CH\(\perp\)AB tại H

Ta có hình vẽ sau:

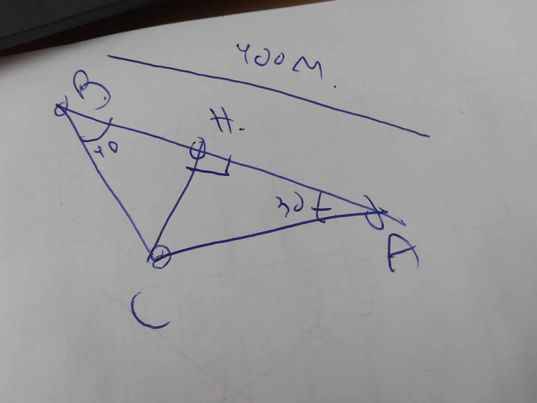
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)

=>\(\widehat{ACB}+30^0+40^0=180^0\)

=>\(\widehat{ACB}=110^0\)

Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)

=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)

=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)

\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)

Xét ΔACB có CH là đường cao

nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)

=>\(CH\cdot\dfrac{400}{2}=27362,57\)

=>\(CH\simeq136,81\left(m\right)\)

Câu 3:

Xét ΔCAB có \(\dfrac{CB}{sinA}=\dfrac{CA}{sinB}\)

=>\(\dfrac{260}{sin45}=\dfrac{CA}{sin30}\)

=>\(CA\simeq183,85\left(m\right)\)

Câu 4:

a: Xét (O) có

ΔACB nội tiếp

AB là đường kính

Do đó: ΔCAB vuông tại C

=>AC\(\perp\)CB tại C

=>AC\(\perp\)EB tại C

Xét ΔABE vuông tại A có AC là đường cao

nên \(BC\cdot BE=BA^2=\left(2R\right)^2=4R^2\)

b: Ta có: ΔOAD cân tại O

mà OE là đường cao

nên OE là phân giác của góc AOD

Xét ΔOAE và ΔODE có

OA=OD

\(\widehat{AOE}=\widehat{DOE}\)

OE chung

Do đó: ΔOAE=ΔODE

=>\(\widehat{OAE}=\widehat{ODE}=90^0\)

Xét tứ giác EAOD có

\(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)

=>EAOD là tứ giác nội tiếp

=>E,A,O,D cùng thuộc một đường tròn

c: Xét (O) có

OD là bán kính

ED\(\perp\)DO tại D

Do đó: ED là tiếp tuyến của (O)

Xét (O) có

\(\widehat{EDC}\) là góc tạo bởi tiếp tuyến DE và dây cung DC

\(\widehat{CBD}\) là góc nội tiếp chắn cung DC

Do đó: \(\widehat{EDC}=\widehat{CBD}\)

=>\(\widehat{EDC}=\widehat{EBD}\)

Xét ΔEDC và ΔEBD có

\(\widehat{EDC}=\widehat{EBD}\)

\(\widehat{DEC}\) chung

Do đó: ΔEDC đồng dạng với ΔEBD

=>\(\widehat{ECD}=\widehat{EDB}\)

Gọi giao điểm của đường nhìn thấy máy bay tại A và B là C.
Vẽ CH vuông góc AB

=>CH là độ cao của máy bay

góc ACB=180-40-32=108 độ

Xét ΔACB có

AB/sin C=AC/sinB=BC/sin A

=>400/sin108=AC/sin32=BC/sin40

=>\(AC\simeq222,9\left(m\right);BC\simeq270,3\left(m\right)\)

\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinC=\dfrac{1}{2}\cdot222.9\cdot270.3\cdot sin108\simeq28650,52\left(m^2\right)\)

Độ cao là:"

28650,52*2/400\(\simeq143\left(m\right)\)

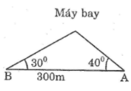
Gọi C là vị trí của máy bay.

Kẻ CH ⊥ AB

Trong tam giác vuông ACH, ta có:

AH = CH.cotgA (1)

Trong tam giác vuông BCH, ta có:

BH = CH.cotgB (2)

Từ (1) và (2) suy ra: (AH + BH) = CH.cotgA + CH.cotgB

Suy ra: CH = 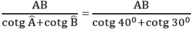 ≈ 102,606 (cm)

Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0

Gọi BC = x => AC = 60 + x

Xét tam giác BDC vuông tại C có:

Xét tam giác ADC vuông tại C có:

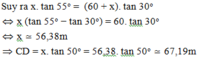
Vậy độ cao của máy bay so với mặt đất là 67,19m

Đáp án cần chọn là: C

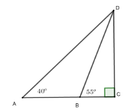
Độ cao của máy bay là CD, độ dài AB = 80m

Gọi BC = x (x > 0) => AC = 80 + x

Xét tam giác BDC vuông tại C có CD = x . tan   55 0

Xét tam giác ADC vuông tại C có CD = (80 + x). tan   44 0

Suy ra  x . tan   55 0 =  (80 + x).  tan   44 0

=> x ≈ 113,96m

=> CD = 113,96. tan   55 0 ≈ 162,75m

Vậy độ cao của máy bay so với mặt đất là 162,75m

Đáp án cần chọn là: A

K/c là \(\dfrac{1700}{\sin25^0}\approx4023\left(m\right)\)