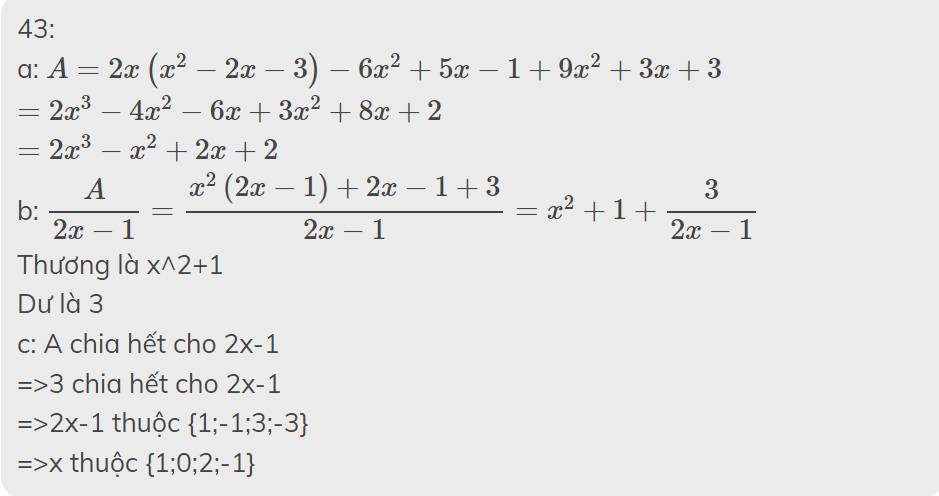Cho biểu thức \(A=\frac{2x^2+3x+3}{2x+1}\)Tìm giá trị nguyên để A nhận giá trị nguyên

Những câu hỏi liên quan
Cho biểu thức A = 2x mũ 2 + 3x+3/2x+1. Tìm giá trị nguyễn x để A nhận giá trị nguyên
Ta có : \(ĐKXĐ:x\ne-\frac{1}{2}\)
\(A=\left(x+1\right)+\frac{2}{2x+1}\) vì \(x\in Z\) nên A nguyên thì \(\frac{2}{2x+1}\) nguyên
Hay \(2x+1\) là ước của 2 . Nên :
\(2x+1=2\Rightarrow x=\frac{1}{2}\) ( loại )
\(2x+1=1\Rightarrow x=0\) ( t/m)
\(2x+1=-1\Rightarrow x=-1\) ( t/m)
\(2x+1=-2\Rightarrow x=-\frac{3}{2}\) ( loại )
Với \(x=0;x=-1\) thì A nhận giá trị nguyên
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
Cho biểu thức: A = (x/x^2-4-4/2-x+1/x+2):3x+3/x^2+2x
a) Tìm điều kiện xác định của A và rút gọn biểu thức A;
b) Tính giá trị của biểu thức A khi |2x-3|-x+1=0
c) Tìm giá trị nguyên của x để A nhận giá trị nguyên.
a: \(A=\left(\dfrac{x}{x^2-4}+\dfrac{4}{x-2}+\dfrac{1}{x+2}\right):\dfrac{3x+3}{x^2+2x}\)
\(=\dfrac{x+4x+8+x-2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x+2\right)}{3\left(x+1\right)}\)
\(=\dfrac{6\left(x+1\right)\cdot x\left(x+2\right)}{3\left(x+1\right)\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{x-2}\)
Đúng 1
Bình luận (0)
Cho biểu thức :
\(A=\left(\frac{x^2-2x}{2x^2+8}-\frac{2x^2}{8-4x+2x^2-x^3}\right)\left(1-\frac{1}{x}-\frac{2}{x^2}\right)\)
a,Tìm x giá trị của A được xác định. Rút gọn biểu thức A
b, Tìm giá trị nguyên của x để A nhận giá rị nguyên
Cho biểu thức A=\(\left(\frac{x^2-2x}{2x^2+8}-\frac{2x^2}{8-4x+2x^2-x^3}\right)\left(1-\frac{1}{x}-\frac{2}{x^2}\right)\)
a) Tìm x để giá trị của A được xác định. Rút gọn biểu thức A
b) Tìm giá trị nguyên của x để A nhận giá trị nguyên
Mọi người giúp mình với ạ!! Mình đang rất cần. Chân thành cảm ơn
43. Cho A = 2x(x + 1)(x-3)-(2x-1)(3x-1) + 3(3x² + x + 1).
a) Rút gọn biểu thức A.
b) Tìm thương và dư khi chia A cho 2x − 1.
c) Tìm giá trị nguyên của x để giá trị của biểu thức A chia hết cho giá trị của biểu thức 2x-1.
Cho biểu thức: A= (2x^2 + 3x + 3)/( 2x + 1). Tìm giá trị của x để A nhận giá trị nguyên.
Các bn giúp mik vs nhé ! Mik cảm ơn trc nha !
Để \(A=\frac{2x^2+3x+3}{2x+1}\)nguyên thì :
\(\left(2x^2+3x+3\right)⋮\left(2x+1\right)\)
\(\left(2x^2+x+2x+1+2\right)⋮\left(2x+1\right)\)
\(\left[x\left(2x+1\right)+\left(2x+1\right)+2\right]⋮\left(2x+1\right)\)
\(\left[\left(2x+1\right)\left(x+1\right)+2\right]⋮\left(2x+1\right)\)
Vì \(\left(2x+1\right)\left(x+1\right)⋮\left(2x+1\right)\)
\(\Rightarrow2⋮\left(2x+1\right)\)
\(\Rightarrow2x+1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow x\in\left\{0;-1;0,5;-1,5\right\}\)
Vậy....
Đúng 0
Bình luận (0)
Cho biểu thức : A= \(\dfrac{1}{x-2}+\dfrac{x^2-2x}{x^2-4}+\dfrac{1}{2+x}\)
a.Tính giá trị của biểu thức A tại x thoả mãn: 2x² + x = 0
b.Tìm x để A= \(\dfrac{-1}{3}\)
c. Tìm x nguyên để A nhận giá trị nguyên
tìm giá trị nguyên của x để biểu thức P = \(\frac{2x^2+3x+3}{2x-1}\)có giá trị nguyên
Để P nguyên => 2x^2 + 3x+3 chia hết cho 2x-1
2x^2+3x+3 = x(2x-1)+4x+3. Vì x(2x-1)chia hết cho 2x-1 => 4x+3 chia hết cho 2x-1
=> 2(2x-1)+5. Do 2(2x-1) chia hết cho 2x-1 nên 5 chia hết cho 2x-1=> 2x-1 thuộc Ư(5)={+-1;+-5}.ta có bảng sau:
| 2x-1 | 1 | -1 | 5 | -5 |
| x | 1 | 0 | 3 | -2 |
Vậy x thuộc{1;0;3;-2} thì P nguyên
Đúng 0
Bình luận (0)
Tìm giá trị nguyên của x để biểu thức \(P=\frac{2x^2+3x+3}{2x-1}\)có giá trị nguyên
\(P=\frac{2x^2-x+4x+3}{2x-1}=\frac{x\left(2x-1\right)+2\left(2x-1\right)+5}{2x-1}\)
\(=x+2+\frac{5}{2x-1}\).Do x nguyên nên x + 2 nguyên.
Để P nguyên thì 2x - 1 thuộc Ư(5).
Đến đây dễ rồi nhé.
Đúng 0
Bình luận (0)
Bài giải
Ta có : \(P=\frac{2x^2+3x+3}{2x-1}=\frac{x\left(2x-1\right)+x+3x+3}{2x-1}=\frac{x\left(2x-1\right)+4x+3}{2x-1}\)
\(=\frac{x\left(2x-1\right)+2\left(2x-1\right)+2+3}{2x-1}=\frac{\left(x+2\right)\left(2x-1\right)+5}{2x-1}=x+2+\frac{5}{2x-1}\)
Để \(P=\frac{2x^2+3x+3}{2x-1}\)nguyên \(\Rightarrow\text{ }\frac{5}{2x-1}\) nguyên \(\Rightarrow\text{ }5\text{ }⋮\text{ }2x-1\)
\(\Leftrightarrow\text{ }2x-1\inƯ\left(5\right)=\left\{\pm1\text{ ; }\pm5\right\}\)
Ta có bảng : ( Vi không có dấu hoặc 4 cái nên mình lập bảng )
| \(2x-1\) | \(-1\) | \(1\) | \(-5\) | \(5\) |
| \(x\) | \(0\) | \(1\) | \(-2\) | \(3\) |
Vậy \(P\) có giá trị nguyên khi \(x\in\left\{0\text{ ; }1\text{ ; }-2\text{ ; }3\right\}\)
Đúng 0
Bình luận (0)




![[MINT HANOUE]](https://hoc24.vn/images/avt/avt83544866_256by256.jpg)