Bài 1 : Cho tam giác MNP vuông tại P, có góc M=60 độ. Tia phân giác của góc NMP cắt NP tại I. Kẻ IK vuông góc với MN (K thuộc MN). Kẻ ND vuông góc với tia MI (D thuộc tia MI). CM
a) MP=MK
b)MI vuông góc với PK
c)Ba đường MP, ND, IK đồng quy.
Những câu hỏi liên quan
Bài 1 : Cho tam giác MNP vuông tại P, có góc M=60 độ. Tia phân giác của góc NMP cắt NP tại I. Kẻ IK vuông góc với MN (K thuộc MN). Kẻ ND vuông góc với tia MI (D thuộc tia MI). CM
a) MP=MK
b)MI vuông góc với PK
c)Ba đường MP, ND, IK đồng quy.
a) Gọi D là giao điểm của PK và MI
Xét ∆ vuông MPI và ∆ vuông MKI ta có :
MI chung
PMI = NMI ( MI là phân giác PMN )
=> ∆MPI = ∆MKI ( ch- gn)
=> MP = MK
=> ∆MDK cân tại M
Vì MI là phân giác PMN
=> MD là trung trực ∆MDK
Đúng 0
Bình luận (0)
cho tam giác MNP vuông tại N có góc M bằng 60 độ. tia phân giác của góc NMP cắt NP ở E . kẻ EK vuông góc với NP (K thuộc MP). Kẻ PT vuông góc với tia ME ( T thuộc tia ME) CM:
a) tam giác MNE = tam giác MKE
và ME vuông góc với NK
b)KM=Kp
c)EP>MN
d) ba đường thẳng MN,PT,KE đồng quy tại 1 điểm
(ko vẽ hình cx dc ạ)
Cho tam giác MNP vuông tại M, Kẻ MI vuông góc với NP tại I. Vẽ MK là tia phân giác của
IMP (K∈IP). Đường thẳng đi qua K và vuông góc với MP, cắt MP tại A.
1) Chứng minh KM là tia phân giác IKA.
2) Chứng minh IK < KP.
3) Gọi giao điểm của AK và MI là B. Chứng minh MK⊥BP và IA//BP.
1: Xét ΔMIK vuông tại I và ΔMAK vuông tại A có
MK chung
góc IMK=góc AMK
=>ΔMIK=ΔMAK
=>góc IKM=góc AKM
=>KM là phân giác của góc AKI
2: KI=KA
KA<KP
=>KI<KP
3: Xét ΔMBP có
PI,BA là đường cao
PI cắt BA tại K
=>K là trực tâm
=>MK vuông góc PB
MI=MA
KI=KA
=>MK là trung trực của AI
=>MK vuông góc AI
=>AI//PB
Đúng 0
Bình luận (0)
Cho tam giác MNP cân tại M có MN =MP 8cm , NP=10cm.
Kẻ MI vuông góc với NP (I thuộc NP)
a chứng minh rằng: IB =IC
b. Kẻ IH vuông góc với MN (H thuộc MN),IK vuông với MP (K thuộc MP). Chứng minh IH=IK
Cho ∆MNP vuông tại M có MN< MP. Kẻ đường phân giác NI của góc MNP ( I thuộc MP) .kẻ IK vuông góc NP a. Chứng minh rằng ∆IMN=∆IKN b. chứng minh rằng MI < IP c. Gọi Q là giao điểm của IK và MN , đường thẳng NI cắt QP tại D. Chứng minh rằng ND vuông góc QP
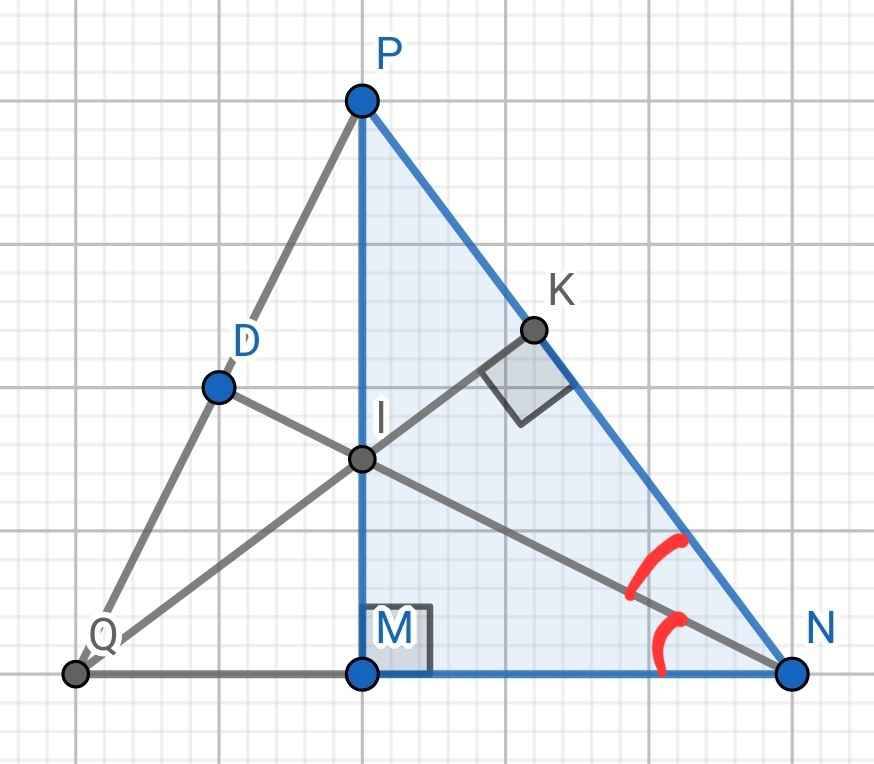
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
Đúng 2
Bình luận (1)
Tam giác MNP có MN = 8 cm , MP = 15 cm , NP = 17 cm.
a) CM tam giác MNP vuông
b) Kẻ tia phân giác NI của góc MNP (I thuộc MP) . Từ I kẻ IK vuông góc ND . CM tam giác MNI = tam giác KNI
c)Tia IK cắt tia NM tại Q . CM KP = MQ
d)Từ M kẻ tia Mx song song IK cắt NI ở H . CM tam giác MIH cân
cho tam giác MNP, có MN < MP. Trên tia NM lấy điểm D sao cho ND=NP. Gọi NE là phân giác của góc MNP (E thuộc MP).. Gọi H là giao điểm của NE và PD. Từ M kẻ MI vuông góc PN tại I. Chứng minh rằng:
a)ED=EP
b) BH vuông góc với PD
c) GÓC DNP = 2.^DMI
Bài 1 : Cho tam giác MNP vuông tại P, có góc M=60 độ. Tia phân giác của góc NMP cắt NP tại I. Kẻ IK vuông góc với MN (K thuộc MN). Kẻ ND vuông góc với tia MI (D thuộc tia MI). CM
a) MP=MK
b)MI vuông góc với PK
c)Ba đường MP, ND, IK đồng quy.
cho tam giác MNP cân tại M coa MN=MP=13cm, NP=10cm. kẻ MI vuông góc với NP (IϵNP)
A, chứng minh rằng: IN=IP
B,tính độ dài MI
C, kẻ IH vuông góc với MN (HϵMN), IK vuông góc với MP (KϵMP).chứng minh IH=IK
Xét tam giác MNI và MPI có
MI là cạnh chung
MN = MP( tam giác MNP cân)
Góc MIN = góc MIP = 90°
=> Tam giác MIN = tam giác MIP( cgv - ch)
IN = IP = 5 cm nên I là trung điểm của NP
b) Tam giác MIN vuông tại I có
NI2 + MI2 = MN2( định lí Pytago)
MI2 + 52 = 142
MI2 + 25 = 196
MI2 = 144
MI=12
c) Xét tam giác PHI và PKI có
MI là cạnh chung
Góc HMI = KMI ( tam giác NMI = PMI )
Góc IHM = IKM = 90°
=》 Tam giác HMI = KMI ( ch - gn)
=》IH=IK
Đúng 2
Bình luận (0)
