Question

Cho ∆MNP vuông tại M có MN< MP. Kẻ đường phân giác NI của góc MNP ( I thuộc MP) .kẻ IK vuông góc NP a. Chứng minh rằng ∆IMN=∆IKN b. chứng minh rằng MI < IP c. Gọi Q là giao điểm của IK và MN , đường thẳng NI cắt QP tại D. Chứng minh rằng ND vuông góc QP

Answer 1

  

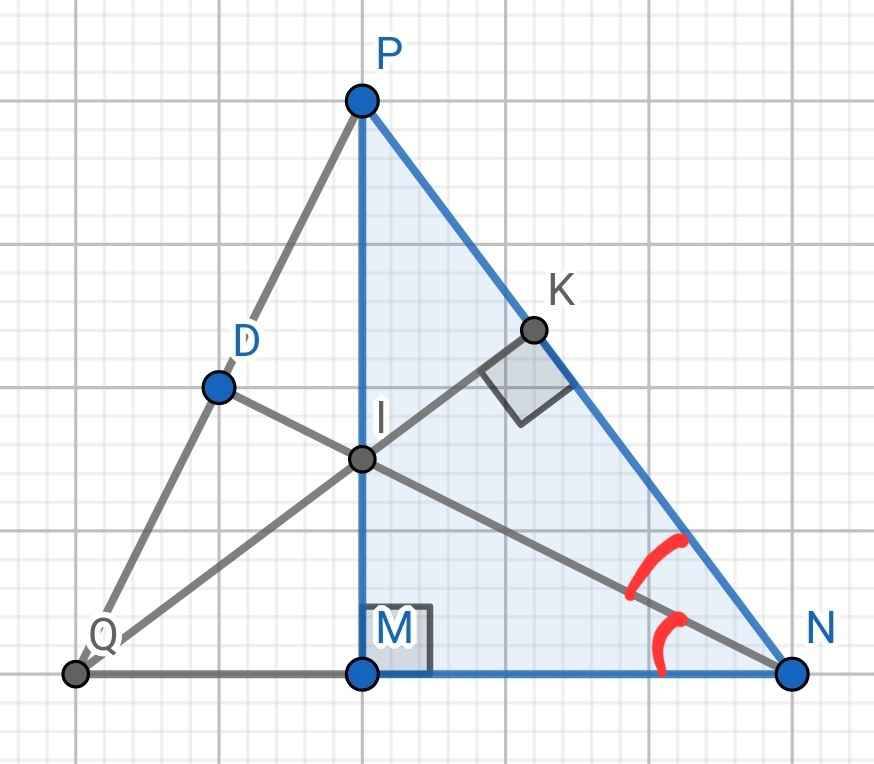
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:

IN chung

MNI = KNI (do NI là phân giác của ∠MNP)

⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)

b) ∆IKP vuông tại K

IP là cạnh huyền nên IP lớn nhất

IK < IP (1)

Do ∆IMN = ∆IKN (cmt)

⇒ MI = IK (2)

Từ (1) và (2)⇒ MI < IP

c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:

IM = IK (cmt)

∠PIK = ∠MIQ (đối đỉnh)

∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)

⇒ KP = MQ (hai cạnh tương ứng)  (3)

Do ∆IMN = ∆IKN (cmt)

⇒ MN = KN (hai cạnh tương ứng)   (4)

Từ (3) và (4) ⇒ KN + KP = MN + MQ

NP = NQ

⇒ ∆NPQ cân tại N

Lại có NI là phân giác của ∠MNP

⇒ NI là phân giác của ∠QNP

⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)

⇒ ND ⊥ QP

Answer 2

Giúp vs ạ mình đang cần gấp