a:

Sửa đề: Chứng minh bốn điểm A,D,H,E cùng nằm trên đường tròn

Xét tứ giác ADHE có

\(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)

=>ADHE là tứ giác nội tiếp đường tròn đường kính AH

=>Tâm O là trung điểm của AH

b: Gọi giao điểm của AH với BC là M

Xét ΔABC có

BD,CE là đường cao

BD cắt CE tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC tại M

OD=OH

=>ΔODH cân tại O

=>\(\widehat{ODH}=\widehat{OHD}\)

mà \(\widehat{OHD}=\widehat{BHM}\)(hai góc đối đỉnh)

và \(\widehat{BHM}=\widehat{BCD}\left(=90^0-\widehat{DBC}\right)\)

nên \(\widehat{ODH}=\widehat{DCB}\)

ΔDBC vuông tại D có DI là đường trung tuyến

nên DI=IB=IC=BC/2

IB=ID

=>ΔIDB cân tại I

=>\(\widehat{IBD}=\widehat{IDB}\)

\(\widehat{ODI}=\widehat{ODB}+\widehat{IDB}\)

\(=\widehat{IBD}+\widehat{DCB}=90^0\)

=>DI là tiếp tuyến của (O)

Ta có H là trực tâm tg ABC

\(\Rightarrow\widehat{EAH}=\widehat{ECB}\left(cùng.phụ.\widehat{ABC}\right)\left(1\right)\)

Mà \(OA=OE\Rightarrow\widehat{AEO}=\widehat{EAO}\left(2\right)\)

Vì EM là tt ứng cạnh huyền BC của tg EBC nên \(EM=MC\)

\(\Rightarrow\widehat{ECM}=\widehat{CEM}\left(3\right)\)

\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{AEO}=\widehat{CEM}\)

Mà \(\widehat{AEO}+\widehat{OEC}=\widehat{AEC}=90^0\Rightarrow\widehat{OEC}+\widehat{CEM}=90^0=\widehat{OEM}\)

Do đó \(OE\perp EM\) hay EM là tt của (O)

Ai giúp em nhanh bài tập này được không ạ?

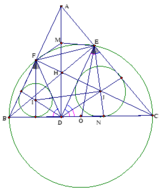
3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF

Tứ giác BFEC có  B E C ^ = B F C ^ = 90 0

=> tứ giác BFEC nội tiếp đường tròn đường kính BC

Gọi O là tâm đường tròn ngoại tiếp tứ giác BFEC thì O cũng là tâm đường tròn ngoại tiếp tam giác BEF

∆ OBE cân tại O (do OB=OE) => O B E ^ = O E B ^

∆ AEH vuông tại E có EM là trung tuyến ứng với cạnh huyền AH (Vì M là trung điểm AH)

=> ME=AH:2= MH do đó  ∆ MHE cân tại M=> M E H ^ = M H E ^ = B H D ^

Mà B H D ^ + O B E ^ = 90 0 ( ∆ HBD vuông tại D)

Nên  O E B ^ + M E H ^ = 90 0 Suy ra  M E O ^ = 90 0

⇒ E M ⊥ O E tại E thuộc ( O ) => EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF

4) Gọi I và J tương ứng là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh DIJ ^   =   DFC ^  

Tứ giác AFDC có A F C ^ = A D C ^ = 90 0  nên tứ giác AFDC nội tiếp đường tròn =>  B D F ^ = B A C ^

∆ BDF và  ∆ BAC có  B D F ^ = B A C ^  (cmt); B ^ chung do đó  ∆ BDF  ~   ∆ BAC(g-g)

Chứng minh tương tự ta có  ∆ DEC ~   ∆ ABC(g-g)

Do đó  ∆ DBF ~ ∆ DEC  ⇒ B D F ^ = E D C ^ ⇒ B D I ^ = I D F ^ = E D J ^ = J D C ^ ⇒ I D J ^ = F D C ^ (1)

Vì  ∆ DBF ~ ∆ DEC (cmt); DI là phân giác, DJ là phân giác  ⇒ D I D F = D J D C  (2)

Từ (1) và (2) suy ra  ∆ DIJ ~ ∆ DFC (c-g-c) =>  DIJ ^   =   DFC ^  

Gọi O là trung điểm của BC

góc AFH+góc AEH=180 độ

=>AFHE nội tiếp đường tròn đường kính AH

=>AFHE nội tiếp (M)

góc BFC=góc BEC=90 độ

=>BFEC nội tiếp đường tròn đường kính BC

=>BFEC nội tiếp (O)

góc MFO=góc MFH+góc OFH

=góc MHF+góc OCF

=góc FBC+góc FCB=90 độ

=>MF là tiếp tuyến của (O)

Xét ΔMFO và ΔMEO có

MF=ME

OF=OE

MO chung

=>ΔMFO=ΔMEO

=>góc MEO=90 độ

=>ME là tiếp tuyến của (O)

Giải thích các bước giải:

a. Gọi OO là trung điểm AHAH

Xét tam giác AEHAEH vuông tại HH: OO là trung điểm AH⇒AO=OH=OEAH⇒AO=OH=OE

Chứng minh tương tự ⇒AO=OH=OD⇒AO=OH=OD

⇒OA=OH=OD=OE⇒OA=OH=OD=OE

Vậy A,D,H,E∈(O)A,D,H,E∈(O) với OO là trung điểm AHAH

b. Có: BD∪CE=H⇒HBD∪CE=H⇒H là trực tâm tam giác ABCABC

⇒AH⊥BC⇒AH⊥BC

Mà: CE⊥ABCE⊥AB

⇒ˆEAH=ˆECB(1)⇒EAH^=ECB^(1) (hai góc có cạnh tương ứng vuông góc)

Có: OA=OE⇒OA=OE⇒ tam giác AOEAOE cân tại OO

⇒ˆAEO=ˆEAO(2)⇒AEO^=EAO^(2)

Chứng minh tương tự ⇒⇒ tam giác EMCEMC cân tại MM

⇒ˆECM=ˆCEM(3)⇒ECM^=CEM^(3)

(1);(2);(3)⇒ˆAEO=ˆCEM(1);(2);(3)⇒AEO^=CEM^

Mà: ˆAEO+ˆOEC=ˆAEC=90∘AEO^+OEC^=AEC^=90∘

⇒ˆOEC+ˆCEM=ˆOEM=90∘⇒OEC^+CEM^=OEM^=90∘

⇒EM⇒EM là tiếp tuyển của (O)(O) 

a: Xét tứ giác ADHE có 

\(\widehat{ADH}+\widehat{AEH}=180^0\)

nên ADHE là tứ giác nội tiếp

hay A,D,H,E cùng thuộc một đường tròn

a: Xét tứ giác ADHE có 

\(\widehat{ADH}+\widehat{AEH}=180^0\)

Do đó: ADHE là tứ giác nội tiếp

hay A,D,H,E cùng thuộc 1 đường tròn