a:

Sửa đề tam giác DEC

Xet ΔABC vuông tại A và ΔDEC vuông tại D có

góc C chung

=>ΔABC đồng dạng với ΔDEC

b: \(BC=\sqrt{3^2+5^2}=\sqrt{34}\left(cm\right)\)

\(AD=\dfrac{2\cdot3\cdot5}{3+5}\cdot cos45=\dfrac{15\sqrt{2}}{8}\left(cm\right)\)

AD là phân giác

=>BD/AB=CD/AC

=>\(\dfrac{BD}{3}=\dfrac{CD}{5}=\dfrac{\sqrt{34}}{8}\)

=>\(BD=\dfrac{3\sqrt{34}}{8}\left(cm\right)\)

Ta có

\(\frac{AD}{DC}=\frac{AB}{BC}=\frac{3}{5}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy)

\(\Rightarrow AB=\frac{3.BC}{5}\)

Ta có

\(BC^2=AB^2+AC^2\) (pitago)

\(\Rightarrow BC^2=\left(\frac{3.BC}{5}\right)^2+\left(AD+DC\right)^2\)

\(\Rightarrow BC^2=\frac{9.BC^2}{25}+64\Rightarrow16.BC^2=1600\Rightarrow BC^2=100\Rightarrow BC=10cm\)

\(AB=\frac{3.BC}{5}=\frac{3.10}{5}=6cm\)

BC=căn 3^2+4^2=5cm

AD là phân giác

=>BD/AB=CD/AC

=>BD/3=CD/4

=>BD/3=CD/4=5/7

=>BD=15/7cm; CD=20/7cm

\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

Xet ΔABC có AD là phân giác

nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7

=>BD=15/7cm; CD=20/7cm

Ai giải giúp vs ạ

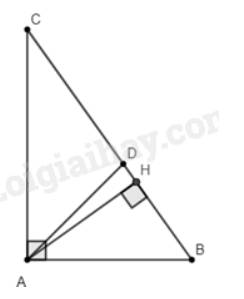
a)

Xét tam giác \(ABC\) vuông tại \(A\) ta có:

\(A{B^2} + A{C^2} = B{C^2}\)

\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)

\( \Leftrightarrow B{C^2} = 25\)

\( \Rightarrow BC = 5cm\)

Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)

Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:

\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)

\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)

\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)

Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).

b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:

\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)

Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)

\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).

Xét tam giác \(AHB\) vuông tại \(H\) ta có:

\(A{H^2} + H{B^2} = A{B^2}\)

\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)

\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)

\( \Leftrightarrow H{B^2} = 3,24\)

\( \Rightarrow HB = 1,8cm\)

\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).

Xét tam giác \(AHD\) vuông tại \(H\) ta có:

\(A{H^2} + H{D^2} = A{D^2}\)

\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)

\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)

\( \Rightarrow AD \approx 2,95cm\)

Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).