Tam giác DEF vuông tại D BIết DE=5cm,cotF=2,4
Tính DF,EF
Cần gấp !
Cho tam giác DEF vuông tại D biết DE = 12cm, DF = 5cm. Tính EF
Áp dụng định lí py - ta - go , ta có :
EF2 = ED2+DF2 = 122 + 52
= 144 + 25 = 169
EF2 = √169 = 13 ( cm )
Xét tam giác DEF vuông tại D
Có: \(DE^2+DF^2=EF^2\left(pitago\right)\)
Thay số\(12^2+5^2=EF^2\)
144+25=EF^2
EF^2=169
EF^2=13^2
=>EF=13
Chúc bn hok tốt
Cho tam giác DEF vuông tại D.Biết DE=5 cotF=2,4
Tính DF,EF
1) Cho tam giác DEF vuông tại D có đường cao DH, Cho DE = 12cm, EF = 20cm. Tính độ dài các
cạnh DF, DH, EH, FH ?
2) Cho tam giác DEF vuông tại D có đường cao DH, Cho EH = 7,2cm, FH = 12,8cm. Tính độ dài
các cạnh EF, DH, DE, DF?
giúp e với ạ e cần gấp
Cho tam giác DEF vuông tại D, đường cao DH. Hãy tính lần lượt độ dài các đoạn EF,DH nếu biết:
a)DE=3cm; DF=4cm
b)DE=12cm;DF=9cm
c)DE=12cm;DF=5cm
a) \(EF=\sqrt{3^2+4^2}=5\)(cm)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{3\cdot4}{5}=\dfrac{12}{5}=2,4\left(cm\right)\)
b) \(EF=\sqrt{12^2+9^2}=15\left(cm\right)\)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cm\right)\)
c) \(EF=\sqrt{12^2+5^2}=13\left(cm\right)\)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{5\cdot12}{13}=\dfrac{60}{13}\left(cm\right)\)
Cho tam giác DEF vuông tại D cs DE=5cm. DF=30dm. Tính EF ( đơn vị cm)
đổi 30dm=3cm
Theo định lý py ta go có
DE2+DF2=EF2
=>25+9=EF2
=>EF2=34
=>EF = căn 34 nhé
Đổi: \(30dm=300cm\)
Áp dụng định lí Pitago vào \(\Delta DEF\left(\widehat{D}=90^o\right)\) có:
\(EF^2=DE^2+DF^2\)
\(\Rightarrow EF=\sqrt{5^2+300^2}=5\sqrt{3601}\left(cm\right)\)
Số xấu vậy?
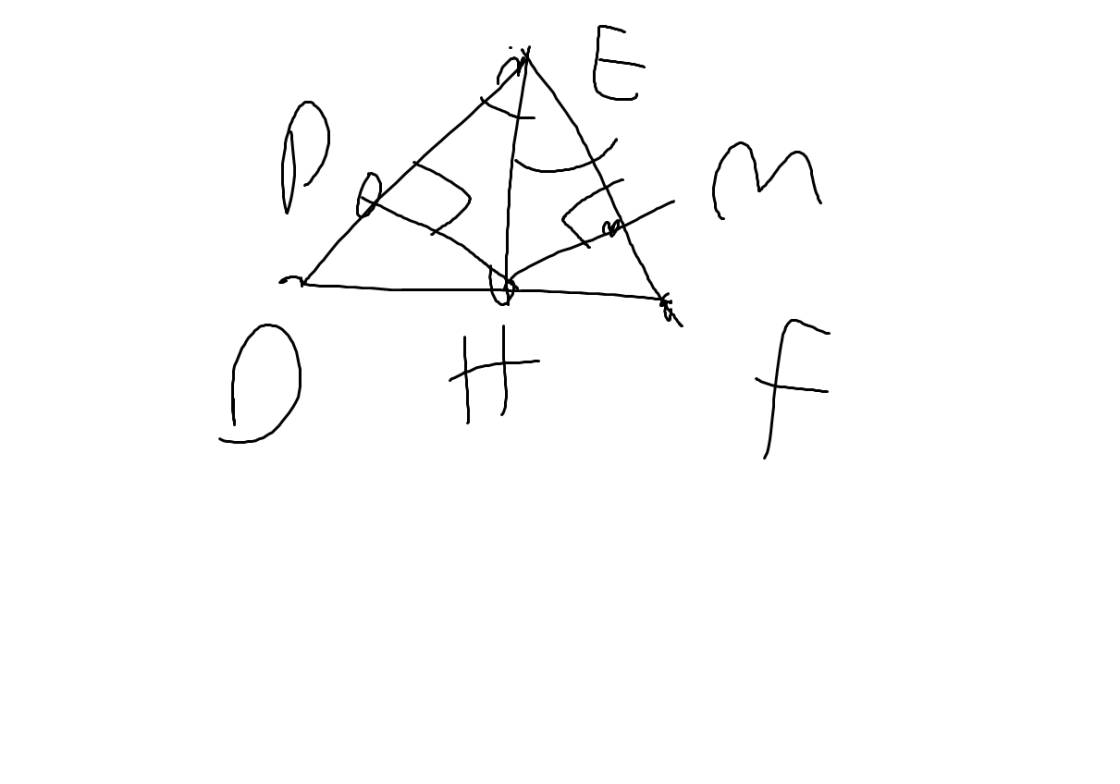
cho tam giác DEF vuông tại D biết DE =5cm;DF=12cm.Kẻ tia phân giác EH (H thuộc DF). Kẻ HN vuông góc EF (N thuộc EF)
a) tính EF
b) chứng minh rằng; tam giác EDH=tam giác ENH
kẻ hình hộ mình luôn nha mấy bạn
a, Xét Δ DEF vuông tại D, có :
\(EF^2=ED^2+DF^2\) (định lí Py - ta - go)
=> \(EF=13\left(cm\right)\)
b, Xét Δ EDH và Δ ENH, có :
\(\widehat{EDH}=\widehat{ENH}=90^o\)
EH là cạnh chung
\(\widehat{DEH}=\widehat{NEH}\) (EH là tia phân giác \(\widehat{EDN}\))
=> Δ EDH = Δ ENH (g.c.g)
a)Áp dụng định lí Pitago
DE2 + DF2 = EF2
hay 52 + 122 = EF2
25 + 144 = \(\sqrt{169}\)
EF = 13cm
b) Xét △ EDH và △ ENH có
EH là cạnh chung
\(\widehat{FDH}=\widehat{FNH}\)
\(\widehat{DEH}=\widehat{NEH}\)
Vậy △ EDH = △ ENH (c-g-c)
a: EF=13cm
b: Xét ΔEDH vuông tại D và ΔENH vuông tại N có
EH chung
\(\widehat{DEH}=\widehat{NEH}\)
Do đó: ΔEDH=ΔENH
Cho tam giác DEF cân tại D, có DE=DF=5cm, góc D=80 độ. Kẻ DH vuông góc với EF(H thuộc EF)
a) Tính số đo góc E
b) Chứng minh EH=HF và góc EDH=góc FDH
c) Tính EF. biết DH=4cm
d) Kẻ HM vuông góc với DE; HN vuông góc với DF. Chứng minh tam giác DMN là tam giác cân tại D
*Vẽ hình dùm mik luôn với!?-
cho tam giác DEF vuông tại có DE<DF.Gọi M là trung điểm EF. Biết DE=3cm, DF=4cm, FE=5cm. Tính DM.
Vì DM là trung tuyến ứng với cạnh huyền EF nên \(DM=\dfrac{1}{2}EF=\dfrac{5}{2}=2,5\left(cm\right)\)
Cho tam giác DEF cân tại E, kẻ EH là phân giác E ( H thuộc DF )
a) Chứng minh tam giác EHD = tam giác EHF
b) Từ H, kẻ HP vuông góc với DE ( P thuộc DF ), HM vuông góc EF ( M thuộc EF )
c) Biết DE = 5cm, DF = 6cm, Tính EH
Vẽ hình giúp mình
a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)