cho tam giác đều ABC có cạnh bằng a ,H là trung điểm của BC.Vecto CH + vecto CH có độ dài là:

Những câu hỏi liên quan
Cho tam giác ABC đều cạnh bằng a, M là trung điểm của BC tính độ dài vecto AM
\(\left|\overrightarrow{AM}\right|=AM=\dfrac{a\sqrt{3}}{2}\)
Đúng 1
Bình luận (0)
Cho tam giác đều ABC có cạnh bằng a H là trung điểm của BC. Độ dài của
C
A
→
-
H
C
→
là
A
.
a
2
B
.
3
a
2
C
.
2...
Đọc tiếp
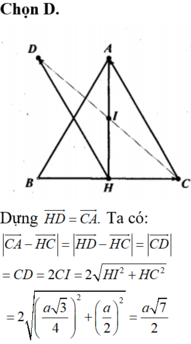
Cho tam giác đều ABC có cạnh bằng a H là trung điểm của BC. Độ dài của C A → - H C → là
A . a 2
B . 3 a 2
C . 2 3 3 a
D . a 7 2
Cho tam giác đều abc có cạnh ab=4cm, gọi M là trung điểm cạnh bc .tính độ dài vecto bm-ba.
\(=\dfrac{4\sqrt{3}}{2}=2\sqrt{3}\)
Đúng 0
Bình luận (0)
cho tam giác đều ABC cạnh a. M là trung điểm AC. Tính độ dài vecto BA+ vecto BM
ΔABC đều có BM là đường trung tuyến
nên BM là phân giác của góc ABC và BM\(\perp\)AC
BM là phân giác của góc ABC
=>\(\widehat{ABM}=\widehat{CBM}=\dfrac{\widehat{ABC}}{2}=30^0\)
M là trung điểm của AC
=>\(AM=MC=\dfrac{AC}{2}=\dfrac{a}{2}\)
ΔAMB vuông tại M
=>\(AM^2+BM^2=AB^2\)
=>\(BM^2=AB^2-AM^2=a^2-\left(0,5a\right)^2=0,75a^2\)
=>\(BM=\dfrac{a\sqrt{3}}{2}\)
Gọi K là trung điểm của AM
=>\(KA=KM=\dfrac{AM}{2}=0,25a\)
ΔBMK vuông tại M
=>\(BM^2+MK^2=BK^2\)
=>\(BK^2=\left(0,25a\right)^2+\left(\dfrac{a\sqrt{3}}{2}\right)^2=\dfrac{13}{16}a^2\)
=>\(BK=\dfrac{a\sqrt{13}}{4}\)
Xét ΔBAM có BK là đường trung tuyến
nên \(\overrightarrow{BA}+\overrightarrow{BM}=2\cdot\overrightarrow{BK}\)
=>\(\left|\overrightarrow{BA}+\overrightarrow{BM}\right|=2\cdot BK=2\cdot\dfrac{a\sqrt{13}}{4}=\dfrac{a\sqrt{13}}{2}\)
Đúng 1
Bình luận (0)
CHo tam giác ABC đều có cạnh là 6. Gọi M, N, P lần lượt là ttrung điểm của AB, AC, BC.
â. kể tên các vectơ bằng vectơ MN
b. tính độ dài vecto MNnhaan độ dài vecto AP
c. hạ PH vuông góc với AC tại H. tính độ dài vecto PH
Cho tam giác abc đều có h là trực tâm của tam giác. Lấy M là trung điểm của AB và biết CM=6cm. Độ dài đoạn CH là
Xem chi tiết
chánnnnnnnnnnnnnnnnnnnnn
Cho tam giác ABC các góc đều nhọn và nội tiếp đường tròn tâm O. H là trực tâm của tam giác ABC.Vẽ đường thẳng AH cắt (O)tại H',cắt BC tại M.E,Flan lượt là trung điểm các cạnh CHva CH'.C/M EF song song và có độ dài bằng HM
Cho tam giác đều ABC có các cạnh bằng 3a, gọi M là trung điểm của BC, I là trung điểm của AM, tính vecto AC x BI
Xem chi tiết
Lời giải:
\(\overrightarrow{AC}.\overrightarrow{BI}=(\overrightarrow{AM}+\overrightarrow{MC})(\overrightarrow{BM}+\overrightarrow{MI})\)
\(=\overrightarrow{AM}.\overrightarrow{BM}+\overrightarrow{AM}.\overrightarrow{MI}+\overrightarrow{MC}.\overrightarrow{BM}+\overrightarrow{MC}.\overrightarrow{MI}\)
\(=\overrightarrow{AM}.\overrightarrow{MI}+\overrightarrow{MC}.\overrightarrow{BM}\)
\(=\overrightarrow{AM}.\frac{-\overrightarrow{AM}}{2}+\frac{\overrightarrow{BC}}{2}.\overrightarrow{BC}=\frac{BC^2-AM^2}{2}\)
\(=\frac{BC^2-(\frac{\sqrt{3}}{2}BC)^2}{2}=\frac{BC^2}{8}=\frac{9a^2}{8}\)
Đúng 0
Bình luận (0)
Cho hình lăng trụ tam giác đều abc.a'b'c' có cạnh đáy bằng a và cạnh bên bằng 2a. Gọi h là trung điểm của cạnh AB
A. Chứng minh CH vuông góc (aa'b'b)
B. tính góc giữa hai mặt phẳng (abc') và (abc')
Xem chi tiết