Cho a,b,c là các số hữu tỉ thỏa mãn a=b+c
Cmr: \(\sqrt{ }\)1/a2 + 1/b2 +1/c2 là 1 số hữu tỉ
Những câu hỏi liên quan
Cho
∫
1
3
3
+
ln
x
(
x
+
1
)
2
d
x
a
ln
3
+
b
ln
2
+
c
với
a
,
b
,
c...
Đọc tiếp
Cho ∫ 1 3 3 + ln x ( x + 1 ) 2 d x = a ln 3 + b ln 2 + c với a , b , c là các số hữu tỉ. Giá trị của a 2 + b 2 + c 2 bằng
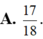
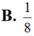
cho a,b là các số hữu tỷ thỏa mãn: (a2+b2-2)(a+b)2+(1-ab)2= -4ab
chứng minh \(\sqrt{1+ab}\) là số hữu tỷ
\(\left(a^2+b^2-2\right)\left(a+b\right)^2+\left(1-ab\right)^2+4ab=0\)
\(\Leftrightarrow\left[\left(a+b\right)^2-2\left(ab+1\right)\right]\left(a+b\right)^2+1+2ab+a^2b^2=0\)
\(\Leftrightarrow\left(a+b\right)^4-2\left(a+b\right)^2\left(ab+1\right)+\left(ab+1\right)^2=0\)
\(\Leftrightarrow\left[\left(a+b\right)^2-\left(ab+1\right)\right]^2=0\)
\(\Leftrightarrow\left(a+b\right)^2-\left(ab+1\right)=0\)
\(\Leftrightarrow ab+1=\left(a+b\right)^2\)
\(\Rightarrow\sqrt{ab+1}=\left|a+b\right|\) là số hữu tỉ (đpcm)
Đúng 1
Bình luận (0)
Cho a,b,c là các số hữu tỉ khác 0 thỏa mãn điều kiện a=b+c
Chứng minh rằng \(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\) là một số hữu tỉ
Ta có: \(a=b+c\Rightarrow c=a-b\)
\(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}=\sqrt{\dfrac{b^2c^2+a^2c^2+a^2b^2}{a^2b^2c^2}}=\sqrt{\dfrac{b^2\left(a-b\right)^2+a^2\left(a-b\right)^2+a^2b^2}{a^2b^2c^2}}=\sqrt{\dfrac{b^4+a^2b^2-2ab^3+a^4+a^2b^2-2a^3b+a^2b^2}{a^2b^2c^2}}=\sqrt{\dfrac{\left(a^2+b^2\right)^2-2ab\left(a^2+b^2\right)+a^2b^2}{a^2b^2c^2}}=\sqrt{\dfrac{\left(a^2+b^2-ab\right)^2}{a^2b^2c^2}}=\left|\dfrac{a^2+b^2-ab}{abc}\right|\)
=> Là một số hữu tỉ do a,b,c là số hữu tỉ
Đúng 2
Bình luận (0)
Cho 3 số hữu tỉ a, b, c thỏa mãn: \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{c}\). CM: \(A=\sqrt{a^2+b^2+c^2}\) là số hữu tỉ
cho a.b là các số hữu tỉ thỏa mãn:\(^{^{a^2}+b^2+\left(\frac{a\cdot b+1}{a+b^2}\right)^2=2.}cmr:\sqrt{a\cdot b+1}\)cũng là số hữu tỉ
\(\Leftrightarrow\left(a+b\right)^2-2\left(ab+1\right)+\left(\frac{ab+1}{a+b}\right)^2=0\)
\(\Leftrightarrow\left(a+b-\frac{ab+1}{a+b}\right)^2=0\)
\(\Leftrightarrow ab+1=\left(a+b\right)^2\Rightarrow\sqrt{ab+1}=a+b\in Q\left(Q.E.D\right)\)
Đúng 0
Bình luận (0)
Cho a, b, c là các số hữu tỉ khác 0 thỏa mãn: a+b+c+d=0. CMR: \(A=\sqrt{\left(ab-cd\right).\left(bc-da\right).\left(ca-bd\right)}\) là số hữu tỉ
Cho
∫
1
3
3
+
ln
x
x
+
1
2
d
x
a
ln
3
+
b
ln
2
+
c
với a,b,c là các số hữu tỉ. Giá trị của
a...
Đọc tiếp
Cho ∫ 1 3 3 + ln x x + 1 2 d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị của a 2 + b 2 - c 2 bằng
A. 17/18
B. 1/8
C. 1.
D. 0.
Cho a, b, c, d là các số hữu tỉ khác 0 thỏa mãn: a+b+c+d=0. CMR: \(A=\sqrt{\left(ab-cd\right).\left(bc-da\right).\left(ca-bd\right)}\) là số hữu tỉ
Cho a, b, c, d là các số hữu tỉ khác 0 thỏa mãn: a+b+c+d=0. CMR: \(A=\sqrt{\left(ab-cd\right).\left(bc-da\right).\left(ca-bd\right)}\) là số hữu tỉ
Bài 1 : Cho a,b,c là các số hữu tỉ thỏa mãn ab+bc+ca=1
CM : Q=\(\sqrt{\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)}\) là 1 số hữu tỉ
thay 1 bởi ab+bc+ca
ta có :Q=\(\sqrt{\left(a^2+ab+bc+ca\right)\left(b^2+ab+bc+ca\right)\left(c^2+ab+bc+ca\right)}\)
ta thấy \(a^2+ab+bc+ca=\left(a+b\right)\left(a+c\right)\)
\(b^2+ab+bc+ca=\left(b+c\right)\left(a+b\right)\)
\(c^2+ab+bc+ca=\left(a+c\right)\left(b+c\right)\)
=> Q= \(\sqrt{\left(a+b\right)^2\left(b+c\right)^2\left(c+a\right)^2}\)=\(\left(a+b\right)\left(b+c\right)\left(c+a\right)\)là một số hữu tỉ vì a,c,b là các số hữu tỉ
Đúng 0
Bình luận (0)
Với ab + ac + bc = 1
Ta có :
a2+1=a2+ab+ac+bc=(a2+ab)+(ac+bc)
=a(a+b)+c(a+b)=(a+c)(a+b)
Tương tự, ta có:
b2+1=(b+a)(b+c)
c2+1=(c+a)(c+b)
Do đó:
(a2+1)(b2+1)(c2+1)=(a+c)(a+b)(b+c)(b+a)(c+a)(c+b)
=(a+b)2(a+c)2(b+c)2=|(a+b)(a+c)(b+c)|
Do a, b, c là số hữu tỷ, do đó :
|(a+b)(a+c)(b+c)| là số hữu tỷ. (đpcm)
Đúng 0
Bình luận (0)