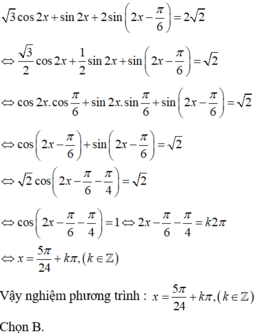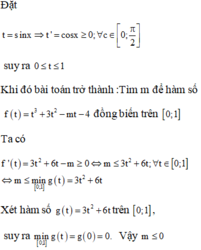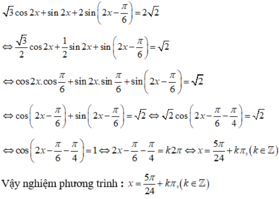Y=sin2x+3cos2x

Những câu hỏi liên quan
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = sin 2 x + 4 sin x . cos x - 3 cos 2 x + 1
Tập giá trị của hàm số y = sin 2 x + 3 cos 2 x + 1 là đoạn a ; b . Tính tổng T = a + b ?
A. T = 0
B. T = 1
C. T = 2
D. T = -1
Đáp án C
Ta có y = sin 2 x + 3 cos 2 x + 1 = 2 sin 2 x + π 3 + 1
Vì
− 1 ≤ sin 2 x + π 3 ≤ 1 ⇒ − 1 ≤ 2 sin 2 x + π 3 + 1 ≤ 3 ⇒ a = − 1 b = 3 ⇒ T = a + b = 2.
Đúng 0
Bình luận (0)
: Tất cả các nghiệm của phương trình: sin2x + sin2x – 3cos2x = 1 là
Giải phương trình
3
cos
2
x
+
sin
2
x
+
2
sin
2
x
-
π
6
2
2
Đọc tiếp
Giải phương trình 3 cos 2 x + sin 2 x + 2 sin 2 x - π 6 = 2 2
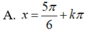
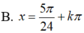
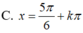
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số
y
sin
2
x
-
3
cos
2
x
-
m
sin
x
-
1
đông biến trên đoạn
0
;
π
2
A. m -3 B. m
≤
0...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = sin 2 x - 3 cos 2 x - m sin x - 1 đông biến trên đoạn 0 ; π 2
A. m > -3
B. m ≤ 0
C. m ≤ -3
D. m > 0
Giải các phương trình sau 3 cos 2 x - 2 sin 2 x + sin 2 x = 1
3 cos 2 x - 2 sin 2 x + sin 2 x = 1
Với cosx = 0 ta thấy hai vế đều bằng 1. Vậy phương trình có nghiệm x = 0,5π + kπ, k ∈ Z
Trường hợp cosx ≠ 0, chia hai vế cho cos2x ta được:
3 - 4 tan x + tan 2 x = 1 + tan 2 x ⇔ 4 tan x = 2 ⇔ tan x = 0 , 5 ⇔ x = a r c tan 0 , 5 + k π , k ∈ Z
Vậy nghiệm của phương trình là
x = 0,5π + kπ, k ∈ Z
và x = arctan 0,5 + kπ, k ∈ Z
Đúng 0
Bình luận (0)
Giải phương trình sau:
3
cos
2
x
+
sin
2
x
+
2
sin
2
x
-
π
6
2
2
A. x ±
5
π
24
+ k2π B. x
5
π...
Đọc tiếp
Giải phương trình sau: 3 cos 2 x + sin 2 x + 2 sin 2 x - π 6 = 2 2
A. x = ± 5 π 24 + k2π
B. x = 5 π 24 + k2π
C. x = 5 π 24 + kπ
D. x = π 6 + kπ
Phương trình :
sin
2
x
-
(
3
+
1
)
sin
x
.
cos
x
+
3
cos
2
x
0
có họ nghiệm là
Đọc tiếp
Phương trình : sin 2 x - ( 3 + 1 ) sin x . cos x + 3 cos 2 x = 0 có họ nghiệm là
![]()
![]()
![]()
![]()
Hướng dẫn giải:
Chọn D.
![]() không là nghiệm của phương trình
không là nghiệm của phương trình
Chia 2 vế phương trình cho cos2x ta được
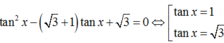
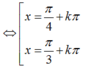
Đúng 0
Bình luận (0)
2sinx -cosx =2
Cos3x+sin3x=1
Sin2x - √3cos2x = 1
√3 sin2x - cosx =1
a.
\(\Leftrightarrow\frac{2}{\sqrt{5}}sinx-\frac{1}{\sqrt{5}}cosx=\frac{2}{\sqrt{5}}\)
Đặt \(\frac{2}{\sqrt{5}}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow sinx.cosa-cosx.sina=cosa\)
\(\Leftrightarrow sin\left(x-a\right)=sin\left(\frac{\pi}{2}-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-a=\frac{\pi}{2}-a+k2\pi\\x-a=\frac{\pi}{2}+a+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=\frac{\pi}{2}+2a+k2\pi\end{matrix}\right.\)
b.
\(\Leftrightarrow\sqrt{2}sin\left(3x+\frac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(3x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\3x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
c.
\(\Leftrightarrow\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x=\frac{1}{2}\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{6}+k2\pi\\2x-\frac{\pi}{3}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
Câu cuối là \(-cosx\) hay \(-cos2x\) bạn?
Đúng 0
Bình luận (0)
Số nghiệm của phương trình sin 2 x + 3 cos 2 x = 3 trên khoảng 0 ; π 2 là?
A. 1
B. 2
C. 3
D. 4
Phương trình ⇔ 1 2 sin 2 x + 3 2 cos 2 x = 3 2 ⇔ sin 2 x + π 3 = 3 2
⇔ sin 2 x + π 3 = sin π 3 ⇔ 2 x + π 3 = π 3 + k 2 π 2 x + π 3 = π − π 3 + k 2 π ⇔ x = k π x = π 6 + k π , k ∈ ℤ .
= 0 < k π < π 2 ⇔ 0 < k < 1 2 → k ∈ ℤ không có giá trị k thỏa mãn.
= 0 < π 6 + k π < π 2 ⇔ − 1 6 < k < 1 3 → k ∈ ℤ k = 0 → x = π 6 .
Chọn đáp án A.
Đúng 0
Bình luận (0)