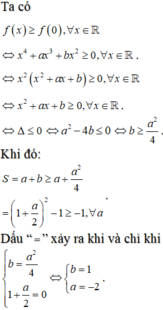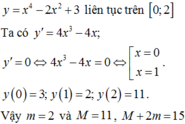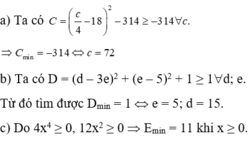Giá trị nhỏ nhất của biểu thức A=x4+2015x2 +3.102 là..........

Những câu hỏi liên quan
Hàm số y = x 4 + a x 3 + b x 2 + 1 đạt giá trị nhỏ nhất tại x=0. Giá trị nhỏ nhất của biểu thức S= a + b là
A. 2
B. 0
C. -2
D. -1
Gọi m là giá trị nhỏ nhất và M là giá trị lớn nhất của hàm số
y
x
4
-
2
x
2
-
3
trên đoạn
0
;
2
. Giá trị biểu thức
M
+
m
bằng A. 2. B. 1 C. -3. D. -7.
Đọc tiếp
Gọi m là giá trị nhỏ nhất và M là giá trị lớn nhất của hàm số y = x 4 - 2 x 2 - 3 trên đoạn 0 ; 2 . Giá trị biểu thức M + m bằng
A. 2.
B. 1
C. -3.
D. -7.
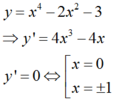
Hàm số đã cho liên tục trên 0 ; 2 có:
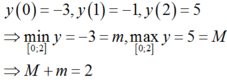
Chọn: A
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A= x4-4x3+7x2-12x+75
Lời giải:
$A=x^4-4x^3+7x^2-12x+75$
$=(x^2-2x)^2+3x^2-12x+75$
$=(x^2-2x)^2+3(x^2-4x+4)+63$
$=(x^2-2x)^2+3(x-2)^2+63\geq 63$
Vậy $A_{\min}=63$. Giá trị này đạt tại $x^2-2x=x-2=0$
$\Leftrightarrow x=2$
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức A= x4-4x3+7x2-12x+75
\(A=\left(x^4-4x^3+4x^2\right)+\left(3x^2-12x+12\right)+63\)
\(A=x^2\left(x^2-4x+4\right)+3\left(x^2-4x+4\right)+63\)
\(A=\left(x^2+3\right)\left(x-2\right)^2+63\ge63\)
\(A_{min}=63\) khi \(x=2\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A=x4+2x2-8x+2019
Giúp mik vs !!!
\(A=x^4+2x^2-8x+2019\) \(=x^4-2x^2+1+4x^2-8x+4+2014\)
\(=\left(x^2-1\right)^2+4\left(x-1\right)^2+2014\ge2014\forall x\)
" = " \(\Leftrightarrow x=1\)
Đúng 2
Bình luận (1)
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y
x
4
-
2
x
2
+
3
trên đoạn [0;2]. Tính giá trị của biểu thức M+2m. A. M+2m13. B. M+2m5. C. M+2m14. D. M+2m15.
Đọc tiếp
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 4 - 2 x 2 + 3 trên đoạn [0;2]. Tính giá trị của biểu thức M+2m.
A. M+2m=13.
B. M+2m=5.
C. M+2m=14.
D. M+2m=15.
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y
x
4
-
2
x
3
+
3
trên đoạn [0; 2]. Tính giá trị của biểu thức M + 2m. A. . B. . C. . D. .
Đọc tiếp
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 4 - 2 x 3 + 3 trên đoạn [0; 2]. Tính giá trị của biểu thức M + 2m.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đáp án D
Ta có ![]() liên tục trên đoạn
liên tục trên đoạn ![]() .
.
Ta có ![]()
 .
.
![]() .
.
Vậy m=2 và M = 11, do đó ![]() .
.
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức B= x4+2016x2+4028 / x2+2
\(B=\dfrac{x^4+2016x^2+4028}{x^2+2}\)
\(=\dfrac{x^4+2x^2+2014x^2+4028}{x^2+2}\)
\(=x^2+2014>=2014\forall x\)
Dấu '=' xảy ra khi x=0
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức sau:
a) A = (x2 - 9)2 + |y - 2| - l; b) B = x4 + 3x2 +2;
a, Có \(\left(x^2-9\right)^2\)≥0 ∀ x ∈ Z
|y-2| ≥0 ∀ y ∈ Z
⇒ Gía trị nhỏ nhất A=-1. Dấu ''='' xảy ra khi:\(\left(x^2-9\right)^2\)+|y-2|=0
⇒ \(x=3\) ; \(y=2\)
Vậy.....
b, Có \(x^4\) ≥ 0 ∀ x ∈ Z
3\(x^2\) ≥ 0 ∀ x ∈ Z
⇒ Giá trị nhỏ nhất của B=2. Dấu ''='' xảy ra khi: \(x^4\)+3\(x^2\)=0
⇒ \(x^2\left(x^2+3\right)\)=0
⇒ \(x^2\) =0
⇒ \(x=0\)
Vậy...
Đúng 2
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức sau:a) C
1
16
c
2
−
9
c
+
10
;
b) D
d
2
+ 10
e
2
– 6de – 10e + 26;c) E 4
x
4
+ 12
x
2
+ 11.
Đọc tiếp
Tìm giá trị nhỏ nhất của các biểu thức sau:
a) C = 1 16 c 2 − 9 c + 10 ; b) D = d 2 + 10 e 2 – 6de – 10e + 26;
c) E = 4 x 4 + 12 x 2 + 11.