Khảo sat sự biến thiên của hàm số: y=\(\sqrt{x-4}\) + \(\sqrt{x+1}\) trên khoảng (4;\(+\infty\))

Những câu hỏi liên quan
Khảo sat sự biến thiên của hàm số: y=\(\sqrt{x-4}\) + \(\sqrt{x+1}\) trên khoảng (4;\(+\infty\))
Một học sinh khảo sát sự biến thiên của hàm số như sau:I. Tập xác định:
D
ℝ
II. Sự biến thiên:
y
x
2
−
x
−
2
;
y
0
⇔
x
−
1
x...
Đọc tiếp
Một học sinh khảo sát sự biến thiên của hàm số như sau:
I. Tập xác định: D = ℝ
II. Sự biến thiên: y ' = x 2 − x − 2 ; y ' = 0 ⇔ x = − 1 x = 2
lim x → − ∞ y = − ∞ ; lim x → + ∞ y = + ∞
III. Bảng biến thiên:
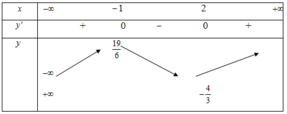
IV. Vậy hàm số đồng biến trên nghịch biến trên khoảng
−
∞
;
−
1
∪
2
;
+
∞
, nghịch biến trên khoảng
−
1
;
2
Lời giải trên sai từ bước nào?
A. Bước IV
B. Bước I
C. Bước II
D. Bước III
Đáp án là D.
• Sai ở bước III (bảng biến thiên)
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên của hàm số sau:
a;y=f(x)=\(\sqrt{x^2+2x+3}\)
b;y=f(x)=\(\sqrt{x^2-3x+2}\)
c;y=f(x)=\(\sqrt{-5x^2+2x+3}\)
khảo sát sự biến thiên và lập bảng biến thiên
y=\(\dfrac{1}{\sqrt{x}-1}\)
cho hàm số y = x3 - 3x2 + mx + 4
1 . khảo sát sự biến thiên và vẽ đồ thị (c) cỏa hàm số đã cho khi m = 0
2 . Tìm M để hàm số nghịch biến trên khoảng \(\left(-1;3\right)\)
+TXĐ: X\(\in\)R
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |
Đúng 0
Bình luận (0)
2. y' = 3x2 - 6x + m <0 khi x thuộc ( -1; 3) => m/3 =-3 => m =-9
Đúng 0
Bình luận (0)
Cho hàm số \(y=\sqrt{x-1}+x^2-2x\)
a, Xét sự biến thiên của hàm số đã cho trên [ 1;+\(\infty\))
b, Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn \(\left[2;5\right]\)
please help me
i need it now
khảo sát sự biến thiên và lập bảng biến thiên
y=\(\sqrt{x}\)
TXĐ: D=[0;+\(\infty\))
Hàm số này luôn đồng biến với mọi x thuộc D
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên của các hàm sốa,ysqrt{x^2+2}b,yx-sqrt{3x+5}trên khoảng left(5;+inftyright)c,yfrac{1}{sqrt{x-1}}d,yfrac{1}{x^2}e,yx^{2015}+1f,yleft|x+2right|-left|x-2right|trên khoảng (-2;2)MÌNH CẦN GẤP GIÚP MÌNH NHA
Đọc tiếp
Khảo sát sự biến thiên của các hàm số
a,\(y=\sqrt{x^2+2}\)
b,\(y=x-\sqrt{3x+5}\)trên khoảng \(\left(5;+\infty\right)\)
c,\(y=\frac{1}{\sqrt{x-1}}\)
d,\(y=\frac{1}{x^2}\)
e,\(y=x^{2015}+1\)
f,\(y=\left|x+2\right|-\left|x-2\right|\)trên khoảng (-2;2)
MÌNH CẦN GẤP GIÚP MÌNH NHA
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau :
a) \(y=x^{\sqrt{3}}\)
b) \(y=x^{\dfrac{1}{\pi}}\)
c) \(y=x^{-e}\)

















