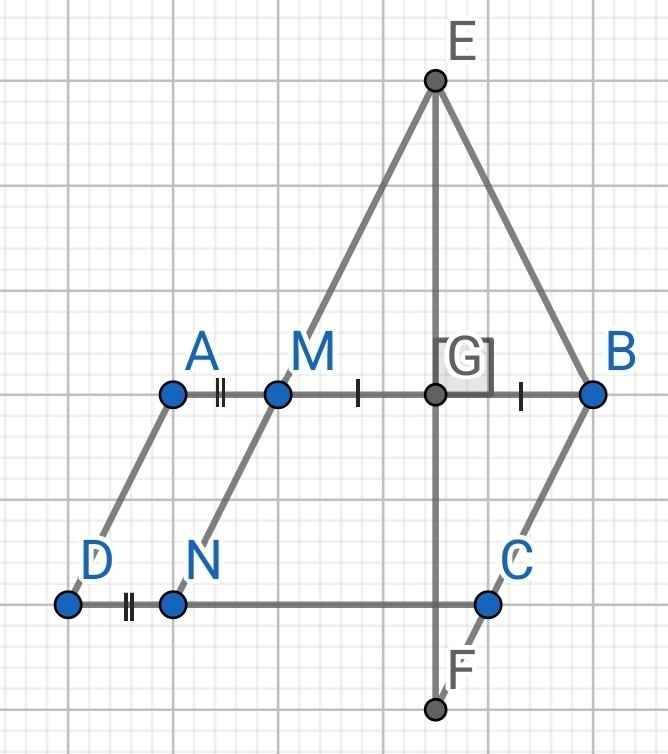
Bài 1: Cho hbh ABCD. Trên các cạnh AB, CD lần lượt lấy các điểm M, N sao cho AM=DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E, F. Chứng minh rằng:
a) E và F đối xứng qua AB
b) MEBF là hình thoi
c) Hbh ABCD phải có thêm điều kiện gì để BCNE là hình thang cân?
Bài 2: Cho tam giác ABC cân tại A. Đường cao AH và E, M thứ tự là trung điểm AB và AC.
a) chứng minh AH là trục đối xứng của tam giác ABC?
b) các tứ giác EMCB, BEMH, AEHM là hình gì? vì sao?
c) tìm điều kiện tam giác ABC để AEHM là hình vuông?
Trong trường hợp này tính diện tích tam giác BHE. Biết AB=4cm
Bài 3: Gọi E, F lần lượt là trung điểm AB, AC của tam giác ABC.
a) Tứ giác EFCB là hình gì? vì sao?
b) CE và BF cắt nhau tại G. Gọi K, H thứ tự là trung điểm của GC và GB. Chứng minh EFKH là hình bình hành.
c) Tìm điều kiện của tam giác ABC để EFKH là hình chữ nhật.
Khi đó so sánh diện tích EFKH với diện tích tam giác ABC
Vẽ hình và giải giúp mình nha. (bài nào làm được thì làm ạ)
Mình đang cần gấp.
Mơn nhìu~~