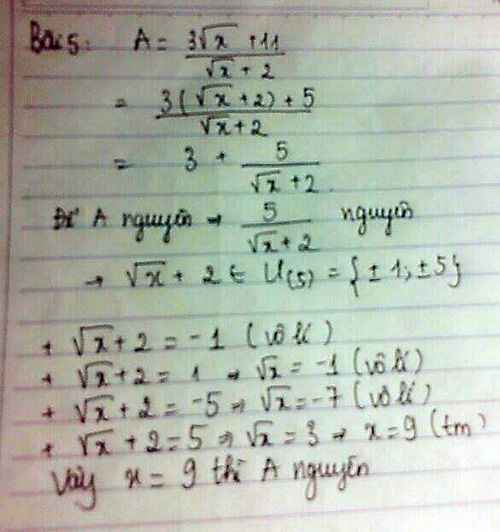a=3√x +11/√x +2

=3(√x +2)+5/√x +2

ĐK: \(x\ge0\)

\(A=\dfrac{3\sqrt{x}+11}{\sqrt{x}+2}\Leftrightarrow A\sqrt{x}+2A=3\sqrt{x}+11\)

\(\Leftrightarrow\left(A-3\right)\sqrt{x}=11-2A\left(1\right)\)

TH1: \(A=3\Rightarrow\) Không tồn tại x thỏa mãn.

TH2: \(A\ne3\)

\(\left(1\right)\Leftrightarrow\sqrt{x}=\dfrac{11-2A}{A-3}\ge0\)

\(\Rightarrow3< A\le\dfrac{11}{2}\)

Vậy \(3< A\le\dfrac{11}{2}\) thì \(A\in Z\).

Lời giải:
a.

Áp dụng BĐT Bunhiacopxky:

$A^2=(\sqrt{x-1}+\sqrt{9-x})^2\leq (x-1+9-x)(1+1)=16$

$\Rightarrow A\leq 4$

Vậy $A_{\max}=4$. Giá trị này đạt tại $x=5$

b.

$A=\frac{3(\sqrt{x}+2)+5}{\sqrt{x}+2}=3+\frac{5}{\sqrt{x}+2}$

Để $A$ nguyên thì $\frac{5}{\sqrt{x}+2}=m$ với $m$ nguyên dương

$\Leftrightarrow \sqrt{x}+2=\frac{5}{m}$

$\sqrt{x}=\frac{5-2m}{m}$

Vì $\sqrt{x}\geq 0$ nên $\frac{5-2m}{m}\geq 0$

Mà $m$ nguyên dương nên $5-2m\geq 0$

$\Leftrightarrow m\leq 2,5$. 

$\Rightarrow m=1; 2$

$\Rightarrow x=9; x=\frac{1}{4}$

Giả sử \(x+\sqrt{2}\) hữu tỉ thì \(x=-\sqrt{2}\) do \(\sqrt{2}\) vô tỉ

Do đó \(x\) vô tỉ

Vậy \(x^3+\sqrt{2}\) vô tỉ

Vậy ko tồn tại số thực x tm đề

Hmm cái này ko chắc :))

\(A=\frac{\sqrt{x}+2}{\sqrt{x}-2}=\frac{\sqrt{x}-2+4}{\sqrt{x}-2}=\frac{\sqrt{x}-2}{\sqrt{x}-2}+\frac{4}{\sqrt{x}-2}=1+\frac{4}{\sqrt{x}-2}\)

Do A nguyên nên \(\frac{4}{\sqrt{x}-2}\) nguyên

\(\Rightarrow\sqrt{x}-2\inƯ\left(4\right)\)

Mà \(\sqrt{x}-2\ge-2\Rightarrow\sqrt{x}-2\in\left\{1;-1;2;-2;4\right\}\)

\(\Rightarrow\sqrt{x}\in\left\{3;1;4;0;6\right\}\)

\(\Rightarrow x\in\left\{9;1;16;0;36\right\}\)

Vậy \(x\in\left\{9;1;16;0;36\right\}\)

a)

Gọi x là số cần tìm, ta có:

 \(x+2>0\left(x>0\right)\)

\(\Rightarrow x-4< 0\)

\(\Rightarrow x< 4\)

\(x=\left\{1;2;3\right\}\)

b)

Gọi x là số cần tìm, khi đó:

\(x-2< 0\left(x< 0\right)\)

\(x+4>0\left(\forall x>-4\right)\)

\(\Rightarrow x=\left(-3;-2;-1\right)\)

a = 2

b = 8

c = 1

d = 7

e = 3

h = 2

trả lời như v k ai hiểu đc