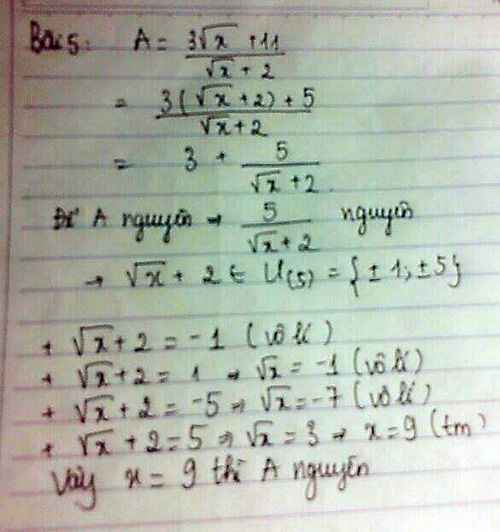Question

Tìm các số hữu tỉ x để \(\dfrac{3\sqrt{x}+11}{\sqrt{x}+2}\)là số nguyên

 

Answer 1

Answer 2

a=3√x +11/√x +2

=3(√x +2)+5/√x +2

Answer 3

ĐK: \(x\ge0\)

\(A=\dfrac{3\sqrt{x}+11}{\sqrt{x}+2}\Leftrightarrow A\sqrt{x}+2A=3\sqrt{x}+11\)

\(\Leftrightarrow\left(A-3\right)\sqrt{x}=11-2A\left(1\right)\)

TH1: \(A=3\Rightarrow\) Không tồn tại x thỏa mãn.

TH2: \(A\ne3\)

 

\(\left(1\right)\Leftrightarrow\sqrt{x}=\dfrac{11-2A}{A-3}\ge0\)

\(\Rightarrow3< A\le\dfrac{11}{2}\)

Vậy \(3< A\le\dfrac{11}{2}\) thì \(A\in Z\).

Answer 4

Lời giải:

Đặt biểu thức là $A$

$A=\frac{3(\sqrt{x}+2)+5}{\sqrt{x}+2}=3+\frac{5}{\sqrt{x}+2}$

Dễ thấy với $x\geq 0$ thì: $A>3$

$\sqrt{x}+2\geq 2\Rightarrow A\leq 3+\frac{5}{2}=\frac{11}{2}$

Vậy $3< A\leq \frac{11}{2}$

$A\in\mathbb{Z}\Leftrightarrow A\in \left\{4;5\right\}$

$\Leftrightarrow 3+\frac{5}{\sqrt{x}+2}\in\left\{4;5\right\}$

$\Leftrightarrow x\in\left\{9; \frac{1}{4}\right\}$