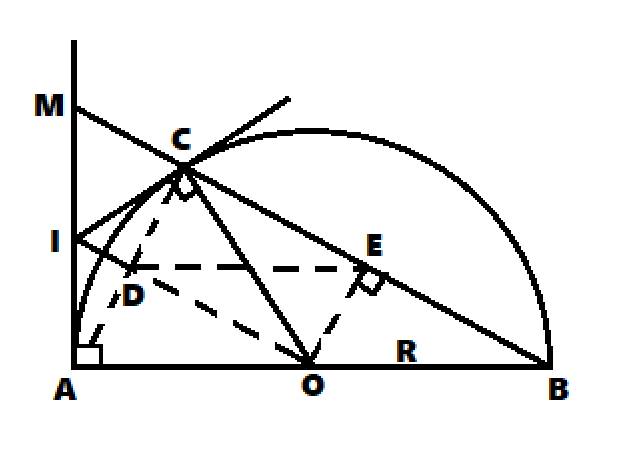
Cho AC là một dây khác đường kính của đường tròn (O) , B là một điểm bất kì trên cung nhỏ AC sao cho AB<AC , kẻ dây BD của đường tròn (O) vuông góc với AC tại H . Gọi I và K lần lượt là hình chiếu của B trên các đường thẳng CD và AD
a) Chứng minh tứ giác BHIC nội tiếp
b) chứng minh 3 điểm H,I,K thẳng hàng
c) Gọi M , N lần lượt là trung điểm của AD và HI . Chứng minh rằng góc BNM =90°