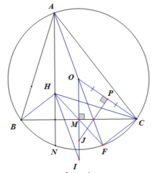
Cho tam giác ABC nhọn (AB < AC) nộp tiếp (O;R), có các đường cao BE, CF cắt nhau tại H. Gọi I,K lần lượt là trung điểm của BC, AH
a/ Chứng minh các tứ giác AEHF, BCEF nội tiếp đường tròn. Suy ra IK vuông góc EF
b/ AH cắt BC tại D. Chứng minh tam giác DEF nội tiếp đường tròn đường kính IK
c/ Các đường thẳng EF, BC cắt nhau tại M. AM cắt (O) tại N. Chứng minh HN vuông góc AM
d/ Kẻ tiếp tuyến tại B của (O) cắt ME tại S. Chứng minh 5 điểm B S N E I cùng thuộc 1 đường tròn