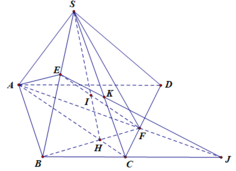
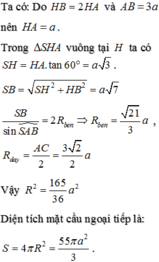Bt3: cho hình chóp S.ABCD có đáy là hình thang cạnh đáy lớn AD.lấy điểm H trên đoạn AC sao cho AH

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy là hình thang đáy lớn AB. Gọi O là giao điểm của AC với BD. H là trung điểm SC. Tìm giao điểm của đường thẳng AH và mp(SBD).
Chọn mp(SAC) có chứa AH
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà S\(\in\)(SAC) giao (SBD)
nên (SAC) giao (SBD)=SO
Gọi K là giao điểm của AH với SO
=>K là giao điểm của AH với mp(SBD)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, đáy nhỏ AB n, đáy lớn CD m (m, n là các số thực dương, m n). Các cạnh bên thỏa mãn SA SB, SC SD. Gọi O là giao điểm hai đường chéo AC và BD. Lấy điểm I trên đoạn SO sao cho IS/IO k. Gọi (alpha) là mặt phẳng đi qua AI và song song với CD. Tìm điều kiện của k để thiết diện của hình chóp S.ABCD với mặt phẳng (alpha) là một hình chữ nhật.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, đáy nhỏ AB = n, đáy lớn CD = m (m, n là các số thực dương, m > n). Các cạnh bên thỏa mãn SA = SB, SC = SD. Gọi O là giao điểm hai đường chéo AC và BD. Lấy điểm I trên đoạn SO sao cho IS/IO = k. Gọi (alpha) là mặt phẳng đi qua AI và song song với CD. Tìm điều kiện của k để thiết diện của hình chóp S.ABCD với mặt phẳng (alpha) là một hình chữ nhật.
Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn AD. Gọi E và F là hai điểm lần lượt nằm trên hai cạnh SB và CD. Gọi H là giao điểm của AC và BF. Tìm giao điểm của EF với mặt phẳng (SAC)
A. Là giao điểm của EF và SH
B. Là giao điểm của EF và HA
C.Là giao điểm của EF và HC
D. Tất cả sai
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
B
A
D
^
60
0
. Hình chiếu vuông góc của S xuống mặt phẳng ABCD là điểm H thuộc đoạn AC sao cho
A
C
⇀
3
A
H...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 0 . Hình chiếu vuông góc của S xuống mặt phẳng ABCD là điểm H thuộc đoạn AC sao cho A C ⇀ = 3 A H ⇀ , mặt phẳng (SBC) tạo với đáy một góc 60 0 . Tính theo a thể tích khối chóp S.ABCD.
A . a 3 3 4
B . a 3 3 12
C . a 3 3 8
D . a 3 3 24
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a. Hình chiếu vuông góc của S trên mặt phẳng đáy ABCD là điểm H thuộc cạnh AB sao cho HB2HA. Cạnh SA hợp với mặt phẳng đáy góc
60
°
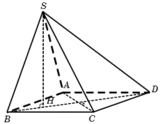
. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a. Hình chiếu vuông góc của S trên mặt phẳng đáy ABCD là điểm H thuộc cạnh AB sao cho HB=2HA. Cạnh SA hợp với mặt phẳng đáy góc 60 ° . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thang(đáy lớn AB). Gọi I, J lần lượt là trung điểm AD và BC , K là điểm trên cạnh SB sao cho SN 32SB . a. Tìm giao tuyến của (SAB) và (IJK)b. Tìm thiết diện của (IJK) với hình chóp S.ABCDTìm điều kiện đểthiết diện là hình bình hành
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang(đáy lớn AB). Gọi I, J lần lượt là trung điểm AD và BC , K là điểm trên cạnh SB sao cho SN = 32SB . a. Tìm giao tuyến của (SAB) và (IJK)b. Tìm thiết diện của (IJK) với hình chóp S.ABCDTìm điều kiện đểthiết diện là hình bình hành
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 1 góc
A
B
C
^
60° Cạnh bên SD
2
. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD 3HB Tính thể tích khối chóp S.ABCD. A.
V
5
24
B.
V
15...
Đọc tiếp
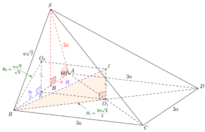
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 1 góc A B C ^ = 60° Cạnh bên SD = 2 . Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB Tính thể tích khối chóp S.ABCD.
A. V = 5 24
B. V = 15 24
C. V = 15 8
D. V = 15 12
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AD.Gọi H,K lần lượt là trung điểm SB, SD, I=AC giao BD. Xét vị trí tương đối của
a) AI và BC
b) HK và BC
c) HK và SI
d) Tìm giao điểm của AH và mp (SBC)
a: \(C\in AI\)
\(C\in BC\)
Do đó: AI cắt BC tại C
b: HK thuộc mp(SBD)
BC thuộc mp(SBC)
Do đó: HK và BC là hai đường chéo nhau
c:Trong mp(SBD), ta có: HK và SI không song song
=>HK cắt SI tại M
d: \(H\in BC\subset\left(SBC\right)\)
\(H\in AH\)
Do đó: AH cắt (SBC)=H
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( đáy lớn AB). Gọi I,J lần lượt là trung điểm của AD và BC, K là điểm trên cạnh SB sao cho SK=2/3SB
a. Tìm giao tuyến của (SAB) và (IJK)
b. Tìm thiết diện của ( IJK) với hình chóp S.ABCD. Tìm điều kiện để thiết diện là hình bình hành