Những câu hỏi liên quan
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
Đề bài thiếu chi tiết định dạng điểm S nên không giải được (ví dụ phải thêm SA vuông góc mặt đáy hoặc gì đó tương tự)
Đúng 0
Bình luận (1)
Cho hình chóp S. ABCD, có đáy hình thang vuông góc tại A và B, AB = BC =a căn3. AD = 2BC, đường thẳng SA vuông góc vs mặt phẳng (ABCD) đg thẳng SC tạo với mp (ABCD) một góc bằng 60đ, gọi E là trung điểm của cạnh SC, tính theo a a) tính thể tích của khối chóp S.ABCD. b) tính thể tích của khối tứ diện EACD. c) kcách từ điểm E đến mp SAD
Xem chi tiết
Cho tam giác ABC có góc A nhỏ hơn 90 độ.Trên nửa mp bờ có chứa C vẽ AD vuông góc AB và AD=Ab.Trên nửa mp AC có chứa B vẽ AE vuông góc vs AC và AE=AC.Qua B vẽ đt song song vs AC.Vẽ Ah vuông góc ED tại H và AH cắt BC tại M và đt song song AC tại F.Chúng minh MB=MC
Gọi A' là điểm đối xứng của A qua M, bạn tự vẽ hình nhé), xét tam giác ADE và tam giác BA'A, có
AB = AD, BA' = AC = AE, góc EAD = EAC + CAD = 90 độ + 90 độ - BAC = 180 độ - BAC = ABA'
Do đó hai tam giác này nbằng nhau theo TH c.g.c
==> DE = AA', mà BACA' là hình bình hành nên AM = 1/2 AA' , đpcm
Dựa vào tíh chất hai tam giác bằng nhau có hai cặp cạnh tương ừng vuông góc thì cặp cạnh còn lại cũng vuông góc, ta CM được AM vuông góc với DE
Đúng 0
Bình luận (0)
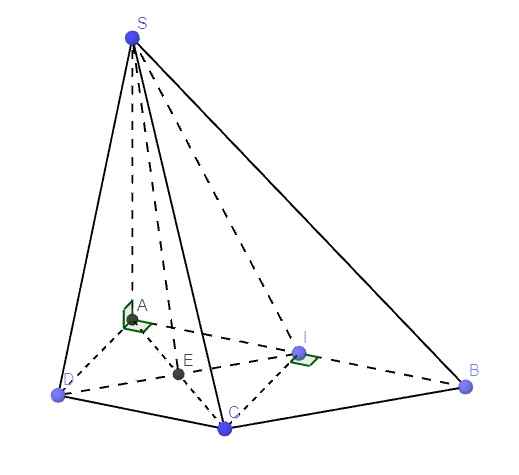
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB. SA vuông góc với (ABCD) a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
c.
Từ câu b ta có AICD là hình vuông \(\Rightarrow CI\perp AB\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CI\)
\(\Rightarrow CI\perp\left(SAB\right)\)
Lại có \(CI\in\left(SCI\right)\Rightarrow\left(SCI\right)\perp\left(SAB\right)\)
d.
I là trung điểm AB \(\Rightarrow CI\) là trung tuyến ứng với AB
Lại có \(CI=AD=a\) (AICD là hình vuông) \(\Rightarrow CI=\dfrac{1}{2}AB\)
\(\Rightarrow\Delta ACB\) vuông tại C
\(\Rightarrow BC\perp AC\) (1)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAC\right)\)
\(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAC\right)\)
Đúng 2
Bình luận (0)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Cho hình bình hành ABCD, phân giác góc A cắt phân giác góc B,D tại P,Q
a,CM PB//DQ và AP vuông góc vs BP,AQ vuông góc vs DQ
b,Phân giác góc C cắt PB,DQ tại M,N.Tứ giác MNPQ là hình gì?Tại sao?
c,CM MP//AD,NQ//AB
d,Giả sử AB>AD.CMR MP=NQ=AB-AD
Bài 1: cho hình thang vuông abcd, BC90° và AD không song song với BC. Trên đường thẳng vuông góc với mp(ABCD) tại B, lấy điểm S và nối S với A,C,D.a) Chứng minh AB⊥mp(SBC)b) Chứng minh mp(SBC) ⊥mp(ABCD).c) Tìm giao tuyến của 2 mặt phẳng (SBC) và (SAD).Bài 2 : Cho hình hộp chữ nhật ABCD.EFGH.a) Đường thẳng BF vuông góc với những mặt phẳng nào?b) CHứng minh mp(AEHD) ⊥mp(CGHD).c) Gọi M, P theo thứ tự là trung điểm của AE,CG. Chứng minh MP//AC.d) Gọi N, Q theo...
Đọc tiếp
Bài 1: cho hình thang vuông abcd, B=C=90° và AD không song song với BC. Trên đường thẳng vuông góc với mp(ABCD) tại B, lấy điểm S và nối S với A,C,D.
a) Chứng minh AB⊥mp(SBC)
b) Chứng minh mp(SBC) ⊥mp(ABCD).
c) Tìm giao tuyến của 2 mặt phẳng (SBC) và (SAD).
Bài 2 : Cho hình hộp chữ nhật ABCD.EFGH.
a) Đường thẳng BF vuông góc với những mặt phẳng nào?
b) CHứng minh mp(AEHD) ⊥mp(CGHD).
c) Gọi M, P theo thứ tự là trung điểm của AE,CG. Chứng minh MP//AC.
d) Gọi N, Q theo thứ tự là trung điểm của BF,DH. Chứng tỏ M,N,P,Q cùng nằm trên 1 mặt phẳng và mp(MNPQ) song song với những mặt phẳng nào?
Cho tam giác ABC nhọn. Trên nửa mp bờ AB chứa C vẽ AD vuông góc vs AB và AD =AB . Trên nửa mp bờ AC chứa c vẽ AE vuông góc vs AC và AE = AC . Kẻ AH vuông góc vs ED tại H . CM : AH đi qua trung điểm BC
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật ,AB=a,AD=a√3 , mp(SAB)vuông góc với đáy và tam giác SAB cân tại S , I là trung điểm AB , K là trung điểm CD góc giữa SB và mp đáy là 45 độ . a) chứng minh SI vuông vs (ABCD) b)chứng minh rằng (SIK)vuông (SCD) c) tính góc giữa SC và (SAB)
a: (SAB) vuông góc (ABCD)
(SAB) giao (ABCD)=AB
SI vuông góc AB
=>SI vuông góc (ABCD)
b: CD vuông góc SI
CD vuông góc IK
=>CD vuông góc (SIK)
=>(SCD) vuông góc (SIK)
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy SA=a căn 3 a)cm SAC vuông góc với SBD b)gọi AH là đg cao của tam giác SAB . cmr AK vuông góc với (SBC) c) tính góc giữa đg thẳng SC và mặt đáy ABC d) tính khoảng cách từ a đến mp (SCD)
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)
Đúng 0
Bình luận (0)