a) Từ giả thiếtta có thể đặt : \(n^2-1=3m\left(m+1\right)\)với m là 1 số nguyên dương

Biến đổi phương trình ta có : 

\(\left(2n-1;2n+1\right)=1\)nên dẫn đến :

TH1 : \(2n-1=3u^2;2n+1=v^2\)

TH2 : \(2n-1=u^2;2n+1=3v^2\)

TH1 :

\(\Rightarrow v^2-3u^2=2\)

\(\Rightarrow v^2\equiv2\left(mod3\right)\)( vô lí )

Còn lại TH2 cho ta \(2n-1\)là số chính phương

b) Ta có : 

\(\frac{n^2-1}{3}=k\left(k+1\right)\left(k\in N\right)\)

\(\Leftrightarrow n^2=3k^2+3k+1\)

\(\Leftrightarrow4n^2-1=12k^2+12k+3\)

\(\Leftrightarrow\left(2n-1\right)\left(2n+1\right)=3\left(2k+1\right)^2\)

- Xét 2 trường hợp :

TH1 : \(\hept{\begin{cases}2n-1=3p^2\\2n+1=q^2\end{cases}}\)

TH2 : \(\hept{\begin{cases}2n-1=p^2\\2n+1=3q^2\end{cases}}\)

+) TH1 :

Hệ \(PT\Leftrightarrow q^2=3p^2+2\equiv2\left(mod3\right)\)( loại, vì số chính phương chia 3 dư 0 hoặc 1 )

+) TH2 :

Hệ \(PT\Leftrightarrow p=2a+1\Rightarrow2n=\left(2a+1\right)^2+1\Rightarrow n^2=a^2+\left(a+1\right)^2\)( đpcm )

Ta có: N = 1.3.5.7.....2013

=> 2N = 2.1.3.5.7.....2013

Vì 2N chia hết cho 2 mà không chia hết cho 4

=> 2N không là số chính phương

Vì 2N chia hết cho 3

=> 2N - 1 chia cho 3 dư 2

=> 2N - 1 không là số chính phương

Vì 2N chia hết cho 2 mà không chia hết cho 4

=> 2N chia cho 4 dư 2

=> 2N + 1 chia cho 4 dư 3

=> 2N + 1 không là số chính phương

Vậy trong 3 số tự nhiên liên tiếp 2N - 1, 2N, 2N + 1 không có số nào là số chính phương.

2. 

Gọi x;x+1;x+2;x+3 là 4 số tự nhiên liên tiếp ( x\(\in\) N)

 Ta có : x (x+1) (x+2 ) (x+3 ) +1 

 =(  x² + 3x ) (x² + 2x + x +2 )  +1 

= (  x² + 3x ) (x² +3x + 2 ) +1  (*)

Đặt t = x² + 3x  thì  (* ) =  t ( t+2 ) + 1=  t² + 2t +1  =  (t+1)²  = (x² + 3x + 1 )²

=>  x (x+1) (x+2 ) (x+3 ) +1  là số chính phương 

hay tích 4 số tự nhiên liên tiếp  cộng  1 là số chính phương 

Gọi x;x+1;x+2;x+3 là 4 số tự nhiên liên tiếp ( x

∈

∈ N)

 Ta có : x (x+1) (x+2 ) (x+3 ) +1 

 =( x2 + 3x ) (x2 + 2x + x +2 ) +1 

= ( x2 + 3x ) (x2 +3x + 2 ) +1 (*)

Đặt t = x2 + 3x thì (* ) = t ( t+2 ) + 1= t2 + 2t +1 = (t+1)2 = (x2 + 3x + 1 )2

=> x (x+1) (x+2 ) (x+3 ) +1 là số chính phương 

hay tích 4 số tự nhiên liên tiếp cộng 1 là số chính phương 

a) Từ giả thiếtta có thể đặt :  \(n^2-1=3m\left(m+1\right)\)  với m là 1 số nguyên dương

Biến đổi phương trình ta có : 

\(\left(2n-1;2n+1\right)=1\) nên dẫn đến :

 \(TH1:2n-1=3u^2;2n+1=v^2\)

\(TH2:2n-1=u^2;2n+1=3v^2\)

\(TH1:\)

\(\Rightarrow v^2-3u^2=2\)

\(\Rightarrow v^2=2\left(mod3\right)\)

Còn lại TH2 cho ta  \(2n-1\) là số chính phương

b) Ta có : 

\(\frac{n^2-1}{3}=k\left(k+1\right)\left(k\in N\right)\)

\(\Leftrightarrow n^2=3k^2+3k+1\)

\(\Leftrightarrow4n^2-1=12k^2+12k+3\)

\(\Leftrightarrow\left(2n-1\right)\left(2n+1\right)=3\left(2k+1\right)^2\)

- Xét 2 trường hợp :

\(TH1:\Rightarrow\hept{\begin{cases}2n-1=3p^2\\2n+1=3q\end{cases}}\)

\(TH2:\Rightarrow\hept{\begin{cases}2n-1=p^2\\2n+1=3q^2\end{cases}}\)

+) TH1 :

Hệ  \(PT\Leftrightarrow q^2=3p^2+2=2\left(mod3\right)\) ( loại, vì số chính phương chia 3 dư 0 hoặc 1 )

+) TH2 :

Hệ  \(PT\Leftrightarrow p=2a+1\Rightarrow2n=\left(2a+1\right)^2+1\Rightarrow n^2=a^2+\left(a+1\right)^2\) ( dpcm )

Ta có: 2N = 2.1.3.5.7.....2013

=> 2N chia hết cho 3

=> 2N - 1 chia cho 3 dư 2

=> 2N - 1 không là SCP

Ta có: N = 1.3.5.7.....2013

=> 2N = 2.1.3.5.7.....2013

Vì 2N chia hết cho 2 mà không chia hết cho 4 => 2N không là SCP

Biết làm mỗi vậy thôi, chờ tí nữa nghĩ tiếp.

2N = 2 . ( 1.3.5.7...2013) 

2N = 2 .4.10 ....4016 

Bài 1: Gọi hai số lẻ liên tiếp là $2k+1$ và $2k+3$ với $k$ tự nhiên.

Gọi $d=ƯCLN(2k+1, 2k+3)$

$\Rightarrow 2k+1\vdots d; 2k+3\vdots d$

$\Rightarrow (2k+3)-(2k+1)\vdots d$

$\Rightarrow 2\vdots d\Rightarrow d=1$ hoặc $d=2$

Nếu $d=2$ thì $2k+1\vdots 2$ (vô lý vì $2k+1$ là số lẻ)

$\Rightarrow d=1$

Vậy $2k+1,2k+3$ nguyên tố cùng nhau. 

Ta có đpcm.

Bài 2:

a. Gọi $d=ƯCLN(n+1, n+2)$

$\Rightarrow n+1\vdots d; n+2\vdots d$

$\Rightarrow (n+2)-(n+1)\vdots d$

$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $(n+1, n+2)=1$ nên 2 số này nguyên tố cùng nhau. 

b.

Gọi $d=ƯCLN(2n+2, 2n+3)$

$\Rightarrow 2n+2\vdots d; 2n+3\vdots d$

$\Rightarrow (2n+3)-(2n+2)\vdots d$ hay $1\vdots d$
$\Rightarrow d=1$.

Vậy $(2n+2, 2n+3)=1$ nên 2 số này nguyên tố cùng nhau.

Bài 2:

c.

Gọi $d=ƯCLN(2n+1, n+1)$

$\Rightarrow 2n+1\vdots d; n+1\vdots d$
$\Rightarrow 2(n+1)-(2n+1)\vdots d$

$\Rightarrow 1\vdots d\Rightarrow d=1$

Vậy $ƯCLN(2n+1, n+1)=1$ nên 2 số này nguyên tố cùng nhau.

d.

Gọi $d=ƯCLN(n+1, 3n+4)$

$\Rightarrow n+1\vdots d; 3n+4\vdots d$

$\Rightarrow 3n+4-3(n+1)\vdots d$

$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $ƯCLN(n+1, 3n+4)=1$

$\Rightarrow$ 2 số này nguyên tố cùng nhau.

Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)

Khi n=1 thì ta sẽ có 1^3=1^2(đúng)

Giả sử (1) đúng khi n=k

Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2

Ta sẽ cần chứng minh (1) đúng khi n=k+1

1^3+2^3+...+n^3

=1^3+2^3+...+k^3+(k+1)^3

=(1+2+3+...+k)^2+(k+1)^3

Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)

=(k+1)^2+2*(k+1)*k*(k+1)/2

=(k+1)^2*(1+k)=(k+1)^3

=>1^3+2^3+...+(k+1)^3

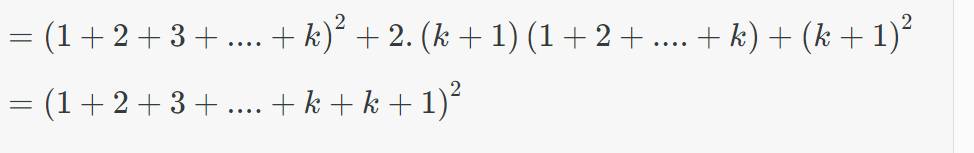
=>ĐPCM