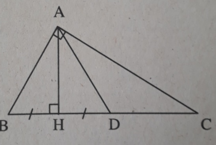
Trên HC lấy D sao cho HD = HB. Tam giác ABD có đường cao AH là trung tuyến nên là tam giác cân, suy ra

∠(ADB) = ∠B . (1)

Ta có: DC = HC – HD = HC – HB = AB = AD ( vì tam giác ABD cân tại A)

Nên ΔADC cân tại D, do đó ∠(DAC) = ∠C (2)

Ta có; ∠ADB + ∠DAC = ∠BAC = 90º (3)

Và ∠B + ∠C = 90º vì tam giác ABC vuông tại A (4)

Từ (2); (3) và (4) suy ra ∠(DAB) = ∠B . (5)

Từ (1) và (5) suy ra ∠(ADB) = ∠B = ∠(DAB) , do đó ΔABD là tam giác đều.

Suy ra AB = BD = AD = DC. Vậy BC = 2AB.

Do HC -HB = AB

Mà HC +HB =BC =>  nhân 2 vế ta có:

HC² -HB² =AB.BC (1).

Áp dụng định lí Pi-ta-go ta có:

HC² =AC²-AH²

HB² = AB² -AH² 

Nên HC² - HB² =AC² -AB² = (BC² -AB² ) -AB² = BC² -2AB² ,(2).

Từ (1 ) và (2 ) có: BC² - 2AB² =AB.BC

                          <=> BC² -AB.BC - 2AB² = 0

                           <=> (BC +AB) (BC -2AB ) = 0,

Do AB +BC >0 nên BC = 2AB.

HC -HB = AB, HC +HB =BC 
nhân 2 vế ta có HC^2 -HB^2 =AB.BC (1). 
Áp dụng Pitago ta có HC ^2 =AC^2-AH^2, HB^2 = AB^2 -AH^2 nên HC^2 - HB^2 =AC^2 -AB^2 = (BC^2 -AB^2 ) -AB^2 = BC^2 -2AB^2 ,(2). Từ (1 ) và (2 ) có BC^2 - 2AB^2 =AB.BC 
<=> BC^2 -AB.BC - 2AB^2 = 0 
<=> (BC +AB) (BC -2AB ) = 0, 
do AB +BC >0 => BC - 2AB = 0 => BC = 2AB.

:3

HC -HB = AB, HC +HB =BC 
Nhân 2 vế ta có HC^2 -HB^2 =AB.BC (1). 

Áp dụng Pitago ta có:

HC² = AC² - AH²; HB² = AB² nên:

HC² - HB² = AC² - AB² = (BC² - AB²) - AB² = BC² - 2AB²

Từ (1) có BC² - 2AB² = AB . BC

<=> BC² - AB . BC - 2AB² = 0

<=> (BC + AB)(BC - 2AB ) = 0, 
Do AB +BC > 0 => BC - 2AB = 0 => BC = 2AB.

theo đề bài ta có BC=BH+HC mà HC-HB=AB nên ta có BC=HB+HC=2(HC-HB) nên ta có BC=2AB  

Cách 1 :

HC -HB = AB, HC +HB =BC
nhân 2 vế ta có HC^2 -HB^2 =AB.BC (1).
Áp dụng Pitago ta có HC ^2 =AC^2-AH^2, HB^2 = AB^2 -AH^2 nên HC^2 - HB^2 =AC^2 -AB^2 = (BC^2 -AB^2 ) -AB^2 = BC^2 -2AB^2 ,(2). Từ (1 ) và (2 ) có BC^2 - 2AB^2 =AB.BC
<=> BC^2 -AB.BC - 2AB^2 = 0
<=> (BC +AB) (BC -2AB ) = 0,
do AB +BC >0 => BC - 2AB = 0 => BC = 2AB

Cách 2:

Dựa vào đường xiên và hình chiếu :
lấy điểm D nằm giữa H,C sao cho HD = HB
==> AB = AD ( do có 2 hình chiếu bằnng nhau )
Đồng thời : AB = HC -- HB ( gt) = HC --HD = CD => AB = CD
nên : AD = CD
Kẻ đường cao DK xuống AC ==> AK = KC (do có 2 đxiên bằng nhau)
Nên K là trung điểm của AC và DK // AB ( do cùng vuông góc AC ) Từ đó D là trung điểm của BC ( đường trung bình )
==> BC = 2. BD = 2. CD , thay CD = AB ta được
----->BC = 2 .AB

mình sẽ chứng minh cho bạn tính chất này trứơc, vì rong bài sẽ có tính chất này

trong 1 tam giác vuông, có góc = 30 độ, thì cạnh góc vuông đối với góc ấy = 1/2 cạnh huyền, vậy cạnh còn lại = ?

giả sử tam giác abc vuông tại a và góc c = 30 dộ, thì ab = 1/2 bc

ta cần tính ac

áp dụng pytago vào tam giác này

\(=>bc^2-ab^2=ac^2\\ < =>4ab^2-ab^2=ac^2\\ < =>3ab^2=ac^2\\ < =>\sqrt{3}.ab=ac\)

thế nhé, giờ mình sẽ àm bài này, mang tinh chất của lớp 8 vì có đồng dạng

theo đề ta có

\(hc-hb=ab\\ < =>\left(hc-hb\right)^2=ab^2\\ < =>hc^2-2.hb.hc+hb^2=ab^2\left(1\right)\)

lại có hb . hc = ah² (2)

ab² = ah² + hb² (3)

từ (1); (2); (3)

\(=>ab^2=hc^2+hb^2-2.hb.hc=ah^2+hb^2\\ < =>ab^2=hc^2+hb^2-2ah^2=ah^2+hb^2\\ < =>ab^2=hc^2-3ah^2\\ < =>hc=\sqrt{3}.ah\)

có cái tính chất nãy mình chứng minh rồi

=> góc c = 30 độ

=> bc = 2 .ab

có mấy cái của lớp 8, nếu ko hiểu thì cứ hỏi mình nhé :)

chúc may mắn

b

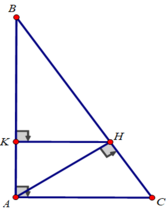
a) Xét tam giác ABC vuông tại A có đường cao AH

⇒ AH2 = HC.HB (1)

Xét tam giác AHB vuông tại H có đường cao HK

⇒ A H 2  = AK.AB (2)

Từ (1) và (2) ⇒ AK.AB = HC.HB