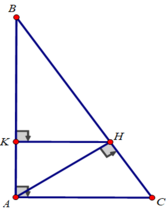
a) Xét tam giác ABC vuông tại A có đường cao AH
⇒ AH2 = HC.HB (1)
Xét tam giác AHB vuông tại H có đường cao HK
⇒ A H 2 = AK.AB (2)
Từ (1) và (2) ⇒ AK.AB = HC.HB
Cho tam giác ABC vuông tại A , AB=3cm,AC= 4cm , đường cao AH .Kẻ HK vuông góc với AC tại K , kẻ HG vuông góc với AB tại G .
a, Chứng minh BH2= AB * BG
b, Chứng minh AC/HC=HB/AK
Cho tam giác ABC vuông tại A, đường cao AH. Gọi HD, HE lần lượt là đường cao của tam giác AHB và tam giác AHC. Chứng minh rằng:
a,\(\frac{AB^2}{AC^2}=\frac{HB}{HC}\)
b,\(\frac{AB^3}{AC^3}=\frac{BD}{EC}\)
Cho tam giác ABC có A = 90 độ , kẻ đường cao AH và trung tuyến AM kẻ HD vuông góc AB , HE vuông góc AC
biết HB = 4,5cm; HC=8cm.
a) Chứng minh BAH = MAC
b) Chứng minh AM vuông góc DE tại K
c) Tính độ dài AK
Cho tam giác ABC vuông tại A, Kẻ đường cao AH. Kẻ HD vuông góc AB, HE vuông góc AC. Chứng minh DE^2 = HB. HC
cho tam giác ABC vuông tại A có AH là đường cao.
a) Kẻ HK vuông góc AB tại K. Cm: AB/HB - HC/AK =0
b)Gọi M, N lần lượt là trung điểm BC và MN cắt AH tại D. Đường thẳng vuông góc với AD tại D cắt AC tại E. Cm: ND2/DC2 (bình phương)+ ND2/ED2(bình phương) = 1
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HK ⊥ AB (K ∈ AB). Chứng minh rằng:
b) A B 2 A C 2 = H B H CCho tam giác ABC vuông tại A, AB = 9cm, AC = 12cm, đường cao AH. Kẻ HK vuông góc với AC tại K, kẻ HG vuông góc với AB tại G.
a)Tính độ dài đoạn AH và các tỉ số lượng giác của góc B ; từ đó suy ra các tỉ số lượng giác của góc C.
b)Chứng minh rằng: AC/HC=HB/AK
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HK ⊥ AB (K ∈ AB). Chứng minh rằng:
c) Cho ∠B = 30 0 , AC = 6 cm. Tính các cạnh AB, BC, AH
Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ HM vuông AB
a) chứng minh: AM x AB = HB . HC
b) Từ C kẻ Cx vuông góc AC tia Cx cắt MH tại N chứng minh: MN mũ 2 = CHxCB
