Tham khảo:

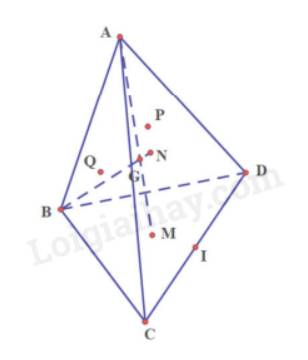
a) Ta có: M là trọng tâm của tam giác BCD

Nên M nằm trên trung tuyến BI (1)

Ta có: N là trọng tâm của tam giác ACD

Nên N nằm trên trung tuyến AI (2)

Từ (1) và (2) suy ra M và N thuộc mp (ABI)

b) Gọi H, K lần lượt là trung điểm của AG, BG

Ta có: HK // AB

          AB // MN

Suy ra MN // HK

Theo định lý Ta-let, ta có: \(\frac{{GM}}{{GH}} = \frac{{GN}}{{GK}} = \frac{{MN}}{{HK}}(1)\)

Ta có:\(\frac{{HK}}{{AB}} = \frac{1}{2},\frac{{MN}}{{AB}} = \frac{1}{3}\)

Do đó \(\frac{{MN}}{{AB}}:\frac{{HK}}{{AB}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{HK}} = \frac{2}{3}(2)\)

Từ (1) và (2) suy ra\(\frac{{GM}}{{GH}} = \frac{2}{3}GH = \frac{1}{2}GA \Rightarrow \frac{{GM}}{{\frac{1}{2}GA}} = \frac{2}{3} \Rightarrow \frac{{GM}}{{GA}} = \frac{1}{3}\)

Chứng minh tương tự ta được\(\frac{{GN}}{{GB}} = \frac{1}{3}\)

c) Gọi H, K lần lượt là trung điểm của BC, BD

Tam giác AHD có:\(\frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)

Suy ra: QM // AD

Do đó, tam giác QGM đồng dạng với tam giác DGA

Nên D, G, Q thẳng hàng

Ta có: QM // AD nên \(\frac{{QM}}{{AD}} = \frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)

Mà \(\frac{{QM}}{{AD}} = \frac{{QG}}{{GD}}\)

Do đó:\(\frac{{QG}}{{GD}} = \frac{1}{3}\)

Chứng minh tương tự ta được\(\frac{{GP}}{{GC}} = \frac{1}{3}\)

Suy ra điều cần chứng minh.

Gọi G lần lượt là trọng tâm tam giác ANP. Ta sẽ chứng minh G cũng là trọng tâm tam giác MQC.
Ta có: \(\overrightarrow{GA}+\overrightarrow{GN}+\overrightarrow{GB}=\overrightarrow{0}\).
Ta cần chứng minh: \(\overrightarrow{GC}+\overrightarrow{GM}+\overrightarrow{GQ}=\overrightarrow{0}\).
Thật vậy: \(\overrightarrow{GC}+\overrightarrow{GM}+\overrightarrow{GQ}=\overrightarrow{GA}+\overrightarrow{AC}+\overrightarrow{GN}+\overrightarrow{NM}+\overrightarrow{GP}+\overrightarrow{PQ}\)
\(=\left(\overrightarrow{GA}+\overrightarrow{GN}+\overrightarrow{GP}\right)+\left(\overrightarrow{AC}+\overrightarrow{NM}+\overrightarrow{PQ}\right)\)
\(=\overrightarrow{0}+\overrightarrow{AC}+\overrightarrow{NM}+\overrightarrow{PQ}\).
Do các điểm M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên PQ và NM lần lượt là các đường trung bình của tam giác DAC và BAC.
Vì vậy: \(\overrightarrow{NM}=\dfrac{1}{2}\overrightarrow{CA};\overrightarrow{PQ}=\dfrac{1}{2}\overrightarrow{CA}\).
Ta có: \(\overrightarrow{AC}+\overrightarrow{NM}+\overrightarrow{PQ}=\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CA}=\overrightarrow{0}\).
Ta chứng minh được: \(\overrightarrow{GC}+\overrightarrow{GM}+\overrightarrow{GQ}=\overrightarrow{0}\) nên G là trọng tâm tam giác CMQ.
Vậy hai tam giác ANP và CMQ có cùng trọng tâm.

a: Gọi giao của AC và BD là O

ABCD là hình bình hành

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

Xét ΔADC có

AN,DO là trung tuyến

AN cắt DO tại F

Do đó: F là trọng tâm cuả ΔADC

Xét ΔABC có

AM,BO là trung tuyến

AM cắt BO tại E

Do đó: E là trọng tâm của ΔABC

b: E là trọng tâm của ΔABC

=>\(BE=\dfrac{2}{3}BO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot BD=\dfrac{1}{3}BD\)

F là trọng tâm của ΔDAC

=>\(DF=\dfrac{2}{3}DO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot BD=\dfrac{1}{3}\cdot BD\)

DF+FE+EB=DB

=>\(FE=DB-\dfrac{1}{3}DB-\dfrac{1}{3}DB=\dfrac{1}{3}DB\)

=>EB=EF=DF

a) Ta có: \(\overrightarrow {EA}  + \overrightarrow {EB}  + \overrightarrow {EC}  + \overrightarrow {ED} \)\( = 4\overrightarrow {EG}  + \overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD} \)

Mà: \(\overrightarrow {GA}  + \overrightarrow {GB}  = 2\overrightarrow {GM} ;\) (do M là trung điểm của AB)

\(\overrightarrow {GC}  + \overrightarrow {GD}  = 2\overrightarrow {GN} \) (do N là trung điểm của CD)

\( \Rightarrow \overrightarrow {EA}  + \overrightarrow {EB}  + \overrightarrow {EC}  + \overrightarrow {ED}  = 4\overrightarrow {EG}  + 2(\overrightarrow {GM}  + \overrightarrow {GN} ) = 4\overrightarrow {EG} \) (do G là trung điểm của MN)

b) Vì E là trọng tâm tam giác BCD nên \(\overrightarrow {EB}  + \overrightarrow {EC}  + \overrightarrow {ED}  = \overrightarrow 0 \)

Từ ý a ta suy ra \(\overrightarrow {EA}  = 4\overrightarrow {EG} \)

c) Ta có: \(\overrightarrow {EA}  = 4\overrightarrow {EG}  \Leftrightarrow \overrightarrow {EA}  = 4.(\overrightarrow {EA}  + \overrightarrow {AG} ) \Leftrightarrow  - 3\overrightarrow {EA}  = 4\overrightarrow {AG} \)

\( \Leftrightarrow 3\overrightarrow {AE}  = 4\overrightarrow {AG} \) hay \(\overrightarrow {AG}  = \frac{3}{4}\overrightarrow {AE} \)

Suy ra A, G, E thẳng hàng và \(AG  = \frac{3}{4}AE \) nên G thuộc đoạn AE.

TK

a, Gọi O là giao điểm hai đường chéo của hình bình hành ABCD

=> O là trung điểm của AC và BD

hay OA = OC và OD = OB

Xét tam giác ADC có:

AF là đường trung tuyến ( F là trung điểm của DC)

DO là đường trung tuyến ( OA=OC)

Hai đường trung tuyến này cắt nhau tại M

=> M là trọng tâm của tam giác ADC

Tương tự, xét tam giác ABC có:

AE là đường trung tuyến ( E là trung điểm của BC)

BO là đường trung tuyến ( OA=OC)

Hai đường trung tuyến cắt nhau tại N

=> N là trọng tâm của tam giác ABC

b, 

Nối M với C ; N với C

Có OM =  OD

ON =  OB

mà OD = OB (cm câu a)

=> OM = ON

Xét tứ giác ANCM có:

OM = ON (cmt)

OA = OC (cm câu a)

=> tứ giác ANCM là hình bình hành

=> AM//CN hay AF//CN

Xét  DNC có:

DF=CF (gt)

MF//CN (AF//CN)

=> DM = MN (1)

Gọi I là giao điểm của EF và MC

Xét  BCD có:

DF = CF (gt)

BE = CE (gt)

=> EF là đường trung bình của  BCD

=> EF//BD

hay EI//BD

Xét  BMC có:

EI//BM ( M BD)

BE = CE (gt)

=> MN = NB (2)

Hầy chỗ này bạn viết đề sai nữa rồi! phải là DM = MN = NB hoặc ngược lại

Từ (1) và (2) suy ra :

DM = MN =NB (đpcm)

hơi dài

Mình sẽ giải cho bạn câu a trước ( tự vẽ hình nha)

Gọi O là giao điểm hai đường chéo của hình bình hành ABCD

=> O là trung điểm của AC và BD

hay OA = OC và OD = OB

Xét tam giác ADC có:

AF là đường trung tuyến ( F là trung điểm của DC)

DO là đường trung tuyến ( OA=OC)

Hai đường trung tuyến này cắt nhau tại M

=> M là trọng tâm của tam giác ADC

Tương tự, xét tam giác ABC có:

AE là đường trung tuyến ( E là trung điểm của BC)

BO là đường trung tuyến ( OA=OC)

Hai đường trung tuyến cắt nhau tại N

=> N là trọng tâm của tam giác ABC

nhưng hơi dài chút

Nối M với C ; N với C

Có \(OM=\dfrac{1}{3}OD\)

ON=\(\dfrac{1}{3}OB\)

mà OD = OB (cm câu a)

=> OM = ON

Xét tứ giác ANCM có:

OM = ON (cmt)

OA = OC (cm câu a)

=> tứ giác ANCM là hình bình hành

=> AM//CN hay AF//CN

Xét  DNC có:

DF=CF (gt)

MF//CN (AF//CN)

=> DM = MN (1)

Gọi I là giao điểm của EF và MC

Xét  BCD có:

DF = CF (gt)

BE = CE (gt)

=> EF là đường trung bình của  BCD

=> EF//BD

hay EI//BD

Xét  BMC có:

EI//BM ( M BD)

BE = CE (gt)

=> MN = NB (2)

Hầy chỗ này bạn viết đề sai nữa rồi! phải là DM = MN = NB hoặc ngược lại

Từ (1) và (2) suy ra :

DM = MN =NB (đpcm)