Cho đa thức B=2x^3+3x^2-29x+30 và hai phân thức
\(\frac{x}{2x^2+7x-15}\); \(\frac{x+2}{x^2+3x-10}\)
a) chia đa thức B lần lượt cho các mẫu thức của hai phân thức đã cho.
b) Quy đồng mẫu thức của hai phân thức đã cho
cho đa thức B=2x3+3x2-29x+30 và hai phân thức
\(\frac{x}{2x^2+7x-15},\frac{x+2}{x^2+3x-10}\)
a)chia đa thức B lần lượt cho các mẫu thức của hai phân thức đã cho
cho đa thức B=2x3+3x2-29x+30 và hai phân thức
\(\dfrac{x}{2x^2+7x-15},\dfrac{x+2}{x^2+3x-10}\)
a)chia đa thức B lần lượt cho các mẫu thức của hai phân thức đã cho
Cho đa thức :
\(B=2x^3+3x^2-29x+30\) và hai phân thức :
\(\dfrac{x}{2x^2+7x-15};\dfrac{x+2}{x^2+3x-10}\)
a) Chia đa thức B lần lượt cho các mẫu thức của hai phân thức đã cho
b) Quy đồng mẫu thức của hai phân thức đã cho
Cho đa thức B = 2 x 3 + 3 x 2 - 29 x + 30 và hai phân thức x 2 x 2 + 7 x - 15 ; x + 2 x 2 + 3 x - 10
Chia đa thức B cho các mẫu thức của hai phân thức đã cho
Cho đa thức B = 2 x 3 + 3 x 2 - 29 x + 30 và hai phân thức x 2 x 2 + 7 x - 15 ; x + 2 x 2 + 3 x - 10
Quy đồng mẫu thức của hai phân thức đã cho.
Mẫu thức chung: 2 x 3 + 3 x 2 - 29 x + 30
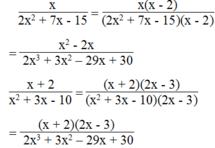
Cho 2 phân thức \(\dfrac{2}{2x^{2^{ }}+7x-15}\),\(\dfrac{x}{x^2+3x-10}\). Chứng tỏ rằng có thể quy đồng mẫu thức của hai phân thức này với mẫu chung là 2x3 + 3x2 - 29x + 30
Lời giải:
Ta có: \(\frac{2}{2x^2+7x-15}=\frac{2}{x(2x-3)+5(2x-3)}=\frac{2}{(2x-3)(x+5)}\)
\(\frac{x}{x^2+3x-10}=\frac{x}{x^2+5x-2x-10}=\frac{x}{x(x+5)-2(x+5)}=\frac{x}{(x-2)(x+5)}\)
Do đó khi quy đồng thì mẫu thức chung của 2 phân số này là:
\((x+5)(2x-3)(x-2)=2x^3+3x^2-29x+30\)
Ta có đpcm.
Phân tích đa thức thành nhân tử
a/ \(5x^2-2x-3\)
b/ \(2x^2-3x-5\)
c/ \(x^2+2x-15\)
d/ \(7x^2-6x-1\)
\(a,=5x^2-5x+3x-3=\left(x-1\right)\left(5x+3\right)\\ b,=2x^2-5x+2x-5=\left(2x-5\right)\left(x+1\right)\\ c,=x^2+5x-3x-15=\left(x+5\right)\left(x-3\right)\\ d,=7x^2-7x+x-1=\left(x-1\right)\left(7x+1\right)\)
c: =(x+5)(x-3)
d: =(x-1)(7x+1)
\(a,5x^2-2x-3=\left(5x^2-5x\right)+\left(3x-3\right)=5x\left(x-1\right)+3\left(x-1\right)=\left(x-1\right)\left(5x+3\right)\\ b,2x^2-3x-5=\left(2x^2+2x\right)-\left(5x+5\right)=2x\left(x+1\right)-5\left(x+1\right)=\left(x+1\right)\left(2x-5\right)\\ c,x^2+2x-15=\left(x^2-3x\right)+\left(5x-15\right)=x\left(x-3\right)+5\left(x-3\right)=\left(x-3\right)\left(x+5\right)\\ d,7x^2-6x-1=\left(7x^2-7x\right)+\left(x-1\right)=7x\left(x-1\right)+\left(x-1\right)=\left(x-1\right)\left(7x+1\right)\)
Cho hai đa thức: A= 5x^4-7x^2+4x+2-3x^3
B= 3x^3+6x^2-5x^4-2x-30
Chứng tỏ rằng hai đa thức trên không đồng thời có giá trị dương tại mỗi giá trị của x
A(x)=5x^4-3x^3-7x^2+4x+2
B(x)=-5x^4+3x^3+6x^2-2x-30
A(x)+B(x)=-x^2+2x-28=-(x-1)^2-27<0
=>A(x) và B(x) ko đồng thời dương
Bài 1:Dùng định nghĩa 2 phân thức bằng nhau, tính A:
a)\(\frac{5x^2-13x+16}{A}\)=\(\frac{5x-3}{2x+5}\)
b)(x^2-3x)/(2x^2-7x+3)=(x^2+4x)/A
Bài 2: Biến đổi mỗi phân thức sau thành 1 phân thức bằng nó và có tử là đa thức A cho trước.
a) (3x-2)/(2x^2+7) và A=3x^2+x-2
b) (x-4)/(x+5) và A=x^2-3x-4