chứng minh công thức thể tích hình nón cụt
V=πh(r12+r22)
Giúp mình vs ạ
Chứng minh công thức tính thể tích hình nón cụt
chứng minh công thức thể tích hình nón cụt
V=1313πh(r12+r22)
Giúp mih đi các bạn ơi
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h=3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P=R+2r
A. 2 3
B. 3.
C. 3 3
D. 2.
Ai giúp em làm bài thuyết trình về hình nón và hình nón cụt với ạ
Cho hình nón đỉnh S có đáy là đường tròn tâm O bán kính R. Trên đường tròn (O) lấy 2 điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng R 2 2 , thể tích V của khối nón đã cho bằng
A. V = π R 3 14 2
B. V = π R 3 14 6
C. V = π R 3 14 3
D. V = π R 3 14 12
1. Hãy phát biểu bằng lời:
a) Công thức tính diện tích xung quanh của hình trụ.
b) Công thức tính thể tích của hình trụ.
c) Công thức tính diện tích xung quanh của hình nón.
d) Công thức tính thể tích của hình nón.
e) Công thức tính diện tích của mặt cầu.
f) Công thức tính thể tích của hình cầu.
a) Diện tích xung quanh hình lăng trụ thì bằng chu vi đường tròn đáy nhân với chiều cao.
b) Thể tích hình trụ thì bằng tích của diện tích hình tròn đáy nhân với đường cao.
c) Diện tích xung quanh hình nón thì bằng 1/2 tích của chu vi đường tròn đáy với đường sinh.
d) Thể tích hình nón bằng 1/3 tích của diện tích hình tròn đáy với chiều cao.
e) Diện tích mặt cầu thì bằng 4 lần diện tích hình tròn lớn.
f) Thể tích hình cầu thì bằng 4/3 tích của diện tích hình tròn lớn với bán kính.
Các bán kính đáy của một hình nón cụt lần lượt là x và 3x, đường sinh là 2,9x. Khi đó thể tích khối nón cụt là.
![]()
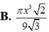
![]()
![]()
Cho hình nón cụt như hình vẽ Biết rằng bán kính của đáy nhỏ là r = 3cm, bán kính của đáy lớn là R = 6cm, độ dài AC = 4cm. Hãy tính diện tích xung quanh, diện tích toàn phần, và thể tích của hình nón cụt

Lời giải:
Diện tích xung quanh hình nón:
$\pi (r+R).l=\pi (6+3).4=36\pi$ (cm vuông)
Diện tích toàn phần:
$36\pi+\pi r^2+\pi R^2=36\pi +\pi.3^2+\pi. 6^2=81\pi$ (cm vuông)
Thể tích:
Chiều cao hình nón: $\sqrt{4^2-(6-3)^2}=\sqrt{7}$ (cm)
$\frac{1}{3}\pi (r^2+R^2+r.R)h=\frac{1}{3}\pi (3^2+6^2+3.6).\sqrt{7}=21\sqrt{7}\pi$ (cm khối)
Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy hai điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng R 2 2 , thể tích hình nón đã cho bằng
A. V = π R 3 14 2
B. V = π R 3 14 6
C. V = π R 3 14 12
D. V = π R 3 14 3