Bạn đổi điểm K thành điểm M là xong nha

Kẻ IG,IK,IH lần lượt vuông góc với AB,BC,AC

Kẻ MO,MD,ME lần lượt vuông góc với AB,BC,AC

Xét ΔBKI vuông tại K và ΔBGI vuông tại G có

BI chung

góc KBI=góc GBI

Do đó: ΔBKI=ΔBGI

Suy ra: IK=IG(1)

Xét ΔCKI vuông tại K và ΔCHI vuông tại H có

CI chung

góc KCI=góc HCI

Do dó: ΔCKI=ΔCHI

Suy ra: IK=IH(2)

Từ (1) và (2) suy ra IG=IH

mà I nằm trong ΔABC và IG,IH là các đường cao ứng với các cạnh AB,AC

nên AI là phân giác của góc BAC(3)

Xét ΔBOM vuông tại O và ΔBDM vuông tại D có

BM chung

góc OBM=góc DBM

Do đó: ΔBOM=ΔBDM

Suy ra: MO=MD(4)

Xét ΔMDC vuông tại D và ΔMEC vuông tại E có

CM chung

góc DCM=góc ECM

Do đó: ΔMDC=ΔMEC

Suy ra: MD=ME(5)

Từ (4) và (5) suy ra MO=ME

mà M nằm ngoài ΔABC và MO,ME là các đường cao ứng với các cạnh AB,AC

nên AM là phân giác của góc BAC(6)

Từ (3) và (6) suy ra A,I,M thẳng hàng

Lời giải:

Kẻ $KM, KT, KN$ lần lượt vuông góc với $AB, AC, BC$.

Vì $K$ thuộc tia phân giác $\widehat{MAC}$ nên $KM=KT$ (tính chất quen thuộc)

Vì $K$ thuộc tia phân giác $\widheat{ACN}$ nên $KN=KT$ 

$\Rightarrow KM=KN$ 

$\Rightarrow K$ thuộc tia phân giác $\widehat{MBN}$ hay $\widehat{ABC}$

Do đó $BI, BK$ cùng là tia phân giác $\widehat{ABC}$

$\Rightarrow B,I,K$ thẳng hàng

Hình vẽ:

Các đường phân giác của các góc ngoài tại đỉnh A và đỉnh C của \(\Delta ABC\)cắt nhau tại K

=> BK là tia phân giác của ^ABC (1)

Các đường phân giác của góc tại đỉnh A và đỉnh C của \(\Delta ABC\)cắt nhau tại I

=> BI là tia phân giác của ^ABC  (2)

Từ (1) và (2) suy ra 3 điểm B,I,K thẳng hành ^^

Cái này bạn đổi điểm K thành điểm M là xong nha

Kẻ IG,IK,IH lần lượt vuông góc với AB,BC,AC

Kẻ MO,MD,ME lần lượt vuông góc với AB,BC,AC

Xét ΔBKI vuông tại K và ΔBGI vuông tại G có

BI chung

góc KBI=góc GBI

Do đó: ΔBKI=ΔBGI

Suy ra: IK=IG(1)

Xét ΔCKI vuông tại K và ΔCHI vuông tại H có

CI chung

góc KCI=góc HCI

Do dó: ΔCKI=ΔCHI

Suy ra: IK=IH(2)

Từ (1) và (2) suy ra IG=IH

mà I nằm trong ΔABC và IG,IH là các đường cao ứng với các cạnh AB,AC

nên AI là phân giác của góc BAC(3)

Xét ΔBOM vuông tại O và ΔBDM vuông tại D có

BM chung

góc OBM=góc DBM

Do đó: ΔBOM=ΔBDM

Suy ra: MO=MD(4)

Xét ΔMDC vuông tại D và ΔMEC vuông tại E có

CM chung

góc DCM=góc ECM

Do đó: ΔMDC=ΔMEC

Suy ra: MD=ME(5)

Từ (4) và (5) suy ra MO=ME

mà M nằm ngoài ΔABC và MO,ME là các đường cao ứng với các cạnh AB,AC

nên AM là phân giác của góc BAC(6)

Từ (3) và (6) suy ra A,I,M thẳng hàng

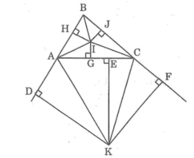
Kẻ IH ⊥ AB, IJ ⊥ BC, IG ⊥ AC, KD ⊥ AB, KE ⊥ AC, KF ⊥ BC

Vì I nằm trên tia phân giác của ∠(BAC) nên IH = IG (tính chất tia phân giác)

Vì I nằm trên tia phân giác của ∠(BCA) nên IJ = IG (tính chất tia phân giác)

Suy ra: IH = IJ

Do đó I nằm trên tia phân giác của ∠(ABC) (1)

Vì K nằm trên tia phân giác của ∠(DAC) nên KD = KE (tính chất tia phân giác)

Vì K nằm trên tia phân giác của ∠(ACF) nên KE = KF (tính chất tia phân giác)

Suy ra: KD = KF

Do đó K nằm trên tia phân giác của ∠(ABC) (2)

Từ (1) và (2) suy ra: B, I, K thẳng hàng.

Các đường phân giác của các góc ngoài tại đỉnh A và C của \(\Delta ABC\) cắt nhau tại K nên BK là tia phân giác của góc B.

Các tia phân giác các góc A và C của \(\Delta ABC\) cắt nhau tại I nên BI là tia phân giác của góc B. Do đó ba điểm B, I, K thẳng hàng.

Kẻ IH ⊥ AB, IJ ⊥ BC, IG ⊥ AC, KD ⊥ AB, KE ⊥ AC, KF ⊥ BC

Vì I nằm trên tia phân giác của ∠(BAC) nên IH = IG (tính chất tia phân giác)

Vì I nằm trên tia phân giác của ∠(BCA) nên IH = IG (tính chất tia phân giác)

Suy ra: IH = IJ

Do đó I nằm trên tia phân giác của (ABC) (1)

Vì K nằm trên tia phân giác của ∠(DAC) nên KD = KE (tính chất tia phân giác)

Vì K nằm trên tia phân giác của ∠(ACF) nên KE = KF (tính chất tia phân giác)

Suy ra: KD = KF

Do đó K nằm trên tia phân giác của ∠(ABC) (2)

Từ (1) và (2) suy ra: B, I, K thẳng hàng.

Tham khảo lời giải tại đây:

https://hoc24.vn/cau-hoi/cho-tam-giac-abc-cac-tia-phan-giac-cac-goc-a-va-c-cat-nhau-o-i-cac-duong-phan-giac-cac-goc-ngoai-tai-dinh-a-va-c-cat-nhau-o-k-chung-minh-rang-3-diem-b-i-k-thang-hang.785122516664

Bạn xem ở đường link này:

Câu hỏi của Cùng học toán đi - Toán lớp 6 - Học toán với OnlineMath