Question

Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng ba điểm B, I, K thẳng hàng.

Answer 1

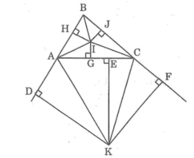
Kẻ IH ⊥ AB, IJ ⊥ BC, IG ⊥ AC, KD ⊥ AB, KE ⊥ AC, KF ⊥ BC

Vì I nằm trên tia phân giác của ∠(BAC) nên IH = IG (tính chất tia phân giác)

Vì I nằm trên tia phân giác của ∠(BCA) nên IJ = IG (tính chất tia phân giác)

Suy ra: IH = IJ

Do đó I nằm trên tia phân giác của ∠(ABC) (1)

Vì K nằm trên tia phân giác của ∠(DAC) nên KD = KE (tính chất tia phân giác)

Vì K nằm trên tia phân giác của ∠(ACF) nên KE = KF (tính chất tia phân giác)

Suy ra: KD = KF

Do đó K nằm trên tia phân giác của ∠(ABC) (2)

Từ (1) và (2) suy ra: B, I, K thẳng hàng.