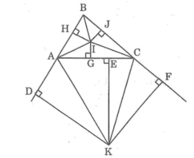
Lời giải:
Kẻ $KM, KT, KN$ lần lượt vuông góc với $AB, AC, BC$.
Vì $K$ thuộc tia phân giác $\widehat{MAC}$ nên $KM=KT$ (tính chất quen thuộc)
Vì $K$ thuộc tia phân giác $\widheat{ACN}$ nên $KN=KT$
$\Rightarrow KM=KN$
$\Rightarrow K$ thuộc tia phân giác $\widehat{MBN}$ hay $\widehat{ABC}$
Do đó $BI, BK$ cùng là tia phân giác $\widehat{ABC}$
$\Rightarrow B,I,K$ thẳng hàng
Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng ba điểm B, I, K thẳng hàng.
Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng 3 điểm B, I, K thẳng hàng.
cho tam giác ABC. Các tia phân giác góc B và góc C cắt nhau tại I. Các đường phân giác các góc ngoài tại đỉnh góc B và góc C cắt nhau ở K. Chứng minh; 3 điểm A,I,K thẳng hàng
Cho tam giác ABC. Các đường phân, giác các góc ngoài tại đỉnh A và C cắt nhau ở K.
a) Cho các tia phân giác các góc A và C trong tam giác ABC cắt nhau ở I Chứng minh B, I, K thẳng hàng.
b) Cho biết A B C ^ = 70 ° . Tính A K C ^ ?
Giúp mk với mn
cho tam giác abc , các tia phân giác của góc A và góc C cắt nhau tại I. Các đường phân giác cắc góc ngoài tại đỉnh A và C cắt nhau ở K . chứng minh 3 điểm Đ I K thẳng hàng
Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhua ở I. Các đường phân giác các góc ngoài tại điỉnh A và C cắt nhau ở K. Chứng minh rằng 3 ddiierm B;I;K thẳng hàng
Cho tam giác ABC.Các tia phân giác của góc B và góc C cắt nhau tại I. Các đường phân giác các góc ngoài tại đỉnh B và C cắt nhau ở K. Chứng minh ba điểm A,I,K thẳng hàng.
Cho tam giác ABC, các tia phân giác góc A và C cắt nhau tại I. Các đường phân giác ngoài tại đỉnh A và C cắt nhau tại K. Chứng minh b,i,k thẳng hàng.
Cho tam giác ABC, các tia phân giác của góc A và C cắt nhau ở I. Các đường phân giác của góc ngoài tại đỉnh A và C cắt nhau ở K. CMR: 3 điểm B, I, K thẳng hàng.
Ai giải nhanh nhất mình tick cho!
