
Những câu hỏi liên quan
Cho ba điểm A, B, C cố định và thẳng hàng theo thứ tự đó. Đường tròn (O; R) thay đổi đi qua B và C sao cho O không thuộc BC. Từ điểm A vẽ hai tiếp tuyến AM và AN với đường tròn (O). Gọi I là trung điểm của BC, E là giao điểm của MN và BC, H là giao điểm của đường thẳng OI và đường thẳng MN. Chứng minh rằng:
a) Bốn điểm M, N, O, I cùng thuộc một đường tròn.
b) OI.OH R2.
c) Đường thẳng MN luôn đi qua một điểm cố định.
Vẽ hình giúp em luôn ạ.
Đọc tiếp
Cho ba điểm A, B, C cố định và thẳng hàng theo thứ tự đó. Đường tròn (O; R) thay đổi đi qua B và C sao cho O không thuộc BC. Từ điểm A vẽ hai tiếp tuyến AM và AN với đường tròn (O). Gọi I là trung điểm của BC, E là giao điểm của MN và BC, H là giao điểm của đường thẳng OI và đường thẳng MN. Chứng minh rằng:
a) Bốn điểm M, N, O, I cùng thuộc một đường tròn.
b) OI.OH = R2.
c) Đường thẳng MN luôn đi qua một điểm cố định.
Vẽ hình giúp em luôn ạ.
Cho ba điểm A, B, C cố định và thẳng hàng theo thứ tự đó. Đường tròn (O;R) thay đổi di chuyển qua B và C sao cho O không thuộc BC. Từ điểm A vẽ hai tiếp tuyến AM và AN với đường tròn (O). a. Cm tg AMON ntb. Cm AB.ACAN2c. Gọi D là trung điểm của BC , đường thẳng ND cắt (O) tại E . Cm ME//ACd. Gọi G,H theo thứ tự là giao điểm của MN với AC và AO . Cm MN luôn đi qua một điểm cố định và tâm đường tròn ngoại tiếp tam giác OHG luôn nằm trên một đường cố đinh (GIÚP Ý c và Ý d với )!!!
Đọc tiếp
Cho ba điểm A, B, C cố định và thẳng hàng theo thứ tự đó. Đường tròn (O;R) thay đổi di chuyển qua B và C sao cho O không thuộc BC. Từ điểm A vẽ hai tiếp tuyến AM và AN với đường tròn (O).
a. Cm tg AMON nt
b. Cm AB.AC=AN2
c. Gọi D là trung điểm của BC , đường thẳng ND cắt (O) tại E . Cm ME//AC
d. Gọi G,H theo thứ tự là giao điểm của MN với AC và AO . Cm MN luôn đi qua một điểm cố định và tâm đường tròn ngoại tiếp tam giác OHG luôn nằm trên một đường cố đinh
(GIÚP Ý c và Ý d với )!!!
Cho ba điểm cố định A, B, C thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi luôn đi qua hai điểm B và C. Vẽ các tiếp tuyến AD, AE với đường tròn (O) (D,E là các tiếp điểm)a) Chứng minh rằng : AD^2AB.AC . Từ đó suy ra D thuộc một đường tròn cố địnhb) Chứng minh rằng đường thẳng DE luôn đi qua một điểm cố định.c) Gọi MN là đường kính đường tròn (O) vuông góc với BC. Gọi K là giao điểm của AM với đường tròn (O). Chứng minh rằng AB, DE, KN, đồng quy.
Đọc tiếp
Cho ba điểm cố định A, B, C thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi luôn đi qua hai điểm B và C. Vẽ các tiếp tuyến AD, AE với đường tròn (O) (D,E là các tiếp điểm)
a) Chứng minh rằng : AD^2=AB.AC . Từ đó suy ra D thuộc một đường tròn cố địnhb) Chứng minh rằng đường thẳng DE luôn đi qua một điểm cố định.c) Gọi MN là đường kính đường tròn (O) vuông góc với BC. Gọi K là giao điểm của AM với đường tròn (O). Chứng minh rằng AB, DE, KN, đồng quy.Cho ba điểm A, B, C cố định và thẳng hàng theo thứ tự đó. Vẽ đường tròn (O) bất kì đi qua B và C sao cho BC không phải là đường kính của (O). Từ A kẻ các tiếp tuyến AE và AF đến (O) với E và F là các tiếp điểm. Gọi I là trung điểm của BC. Gọi D là giao điểm thứ hai của đường thẳng FI và (O). Chứng minh : ED//AC và AH.AI=AB.AC.

gọi Ex là tia đối của tiếp tuyến EA
Ta có : \(\widehat{xED}=\frac{1}{2}sđ\widebat{ED}\); \(\widehat{EFD}=\frac{1}{2}sđ\widebat{ED}\)\(\Rightarrow\widehat{xED}=\widehat{EFD}\)( 1 )
Dễ thấy tứ giác AFOE nội tiếp
I là trung điểm của BC nên OI \(\perp\)BC \(\Rightarrow\)tứ giác AIOE nội tiếp
\(\Rightarrow\)5 điểm A,F,I,O,E cùng thuộc 1 đường tròn
\(\Rightarrow\)tứ giác AFIE nội tiếp \(\Rightarrow\)\(\widehat{EAI}=\widehat{EFI}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra : \(\widehat{xED}=\widehat{EAI}\Rightarrow ED//AC\)
Gọi N là giao điểm của AO và EF
Dễ chứng minh AN \(\perp\)EF
\(\DeltaẠNH~\Delta AIO\left(g.g\right)\Rightarrow\frac{AN}{AH}=\frac{AI}{AO}\Rightarrow AI.AH=AN.AO\)( 3 )
Ta có : \(AE^2=AN.AO\)( 4 )
Xét \(\Delta AEB\)và \(\Delta ACE\)có :
\(\widehat{EAC}\)( chung ) ; \(\widehat{AEB}=\widehat{ACE}=\frac{1}{2}sđ\widebat{EB}\)
\(\Rightarrow\Delta AEB~\Delta ACE\left(g.g\right)\)
\(\Rightarrow\frac{AE}{AB}=\frac{AC}{AE}\Rightarrow AE^2=AB.AC\)( 5 )
Từ ( 3 ) , ( 4 ) và ( 5 ) suy ra : AH.AI = AB.AC
đề bạn cho thiếu nhé. đoạn cuối AH. AI = AB . AC với H là giao điểm của AC và EF

Mượn tạm hình anh Thanh Tùng DZ tý :)) Không biết cách làm của em có khác gì của anh không,anh check giúp em ạ :D
Ta có ED // AC ( theo chứng minh của anh Tùng )
Xét phương tích điểm A với ( O ) ta có:\(AB.AC=AF^2\)
Ta cần chứng minh \(AH.AI=AF^2\)
Ta có:\(\widehat{AFH}=\widehat{FDE}=\widehat{FIA}\)
Khi đó \(\Delta\)AFH ~ \(\Delta\)AIF ( g.g ) nên \(AH.AI=AF^2\)
=> ĐPCM
Xem thêm câu trả lời
Cho 3 điểm A,B,C cố định, thẳng hàng theo thứ tự đó. Vẽ đường tròn (O) đi qua B,C. Từ A kẻ tiếp tuyến AM,AN với (O) (M,N là các tiếp điểm). Gọi I là trung điểm BC. Đường thẳng AO cắt MN tại H. Đường thẳng NI cắt đường tròn tại điểm thứ 2 D.1. CMR AMIN là tứ giác nội tiếp2. CMR MD//BC3 CM khi (O) thay đổi nhưng luôn đi qua B,C (với O không thuộc BC) thì N thuộc một đường tròn cố định và tâm đường tròn ngoại tiếp tam giác HIO chạy trên 1 đường thẳng cố định
Đọc tiếp
Cho 3 điểm A,B,C cố định, thẳng hàng theo thứ tự đó. Vẽ đường tròn (O) đi qua B,C. Từ A kẻ tiếp tuyến AM,AN với (O) (M,N là các tiếp điểm). Gọi I là trung điểm BC. Đường thẳng AO cắt MN tại H. Đường thẳng NI cắt đường tròn tại điểm thứ 2 D.
1. CMR AMIN là tứ giác nội tiếp
2. CMR MD//BC
3 CM khi (O) thay đổi nhưng luôn đi qua B,C (với O không thuộc BC) thì N thuộc một đường tròn cố định và tâm đường tròn ngoại tiếp tam giác HIO chạy trên 1 đường thẳng cố định
Cho ba điểm A,B,C cố định, thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi nhưng luôn đi qua hai điểm C và B ( O không thuộc BC). Từ A vẽ hai tiếp tuyến AM và AN với đường tròn (O) ( M. N là hai tiếp điểm). Gọi I là trung điểm của BC.1) Chứng minh bốn điểm O, I, A, M cùng thuộc một đường tròn.2) Gọi E, H lần lượt là giao điểm của OA với đường tròn (O) và MN. Chứng minh BE là tia phân giác của góc ABH.3) Chứng minh rằng tâm của đường tròn ngoại tiếp tam giác OHI luôn nằm trên một đường...
Đọc tiếp
Cho ba điểm A,B,C cố định, thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi nhưng luôn đi qua hai điểm C và B ( O không thuộc BC). Từ A vẽ hai tiếp tuyến AM và AN với đường tròn (O) ( M. N là hai tiếp điểm). Gọi I là trung điểm của BC.
1) Chứng minh bốn điểm O, I, A, M cùng thuộc một đường tròn.
2) Gọi E, H lần lượt là giao điểm của OA với đường tròn (O) và MN. Chứng minh BE là tia phân giác của góc ABH.
3) Chứng minh rằng tâm của đường tròn ngoại tiếp tam giác OHI luôn nằm trên một đường thẳng cố định
GIẢI PHÁP CỦA CÂU NÀY LÀ GHÕ CHO MẠNG
Cho ba điểm A,B,C cố định thẳng hàng theo thứ tự đó. Đường tròn tâm O di động luôn đi qua B, C. kẻ qua A các tiếp tuyến AE, AF đến đường tròn tâm O. Gọi E,F là hai tiếp điểm . Gọi I là trung điểm của BC và K là giao của FI với đường tròn tâm O. CMR: véc tơ EK và véc tơ AB cùng phương
a) Vì tam giác AFB đồng dạng với ACF(g.g) nên:
AF/AC=AB/AF hay AF^2=AB.AC => AF=căn(AB.AC) ko đổi 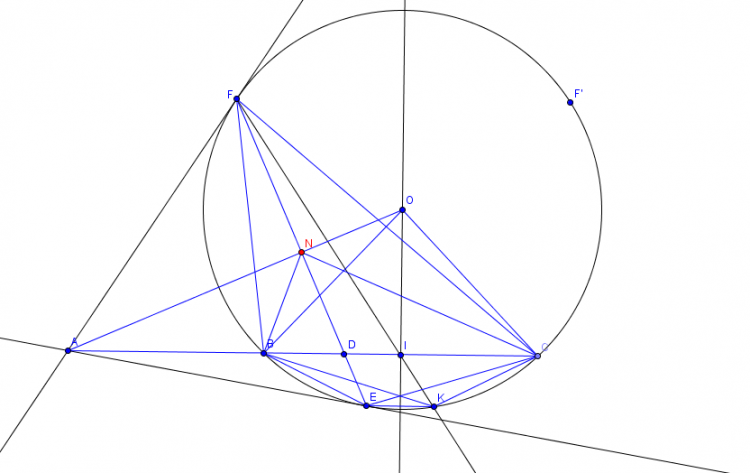
Mà AE=AF (T/cTtuyen) nên E, F cùng thuộc đường tròn bán kính căn(AB.AC)
b)Ta có: OI vuông góc với BC (T/ đường kính và dây)
Các điểm E, F, I cùng nhìn OA dưới 1 góc ko đổi 90 độ nên O,I,F,A,E cùng thuộc đường tròn đường kính OA
Ta có góc FIA=FOA(Cùng chắn cung FA trong đường tròn (OIFAE)
Mà góc FKE=FOA( Cùng bằng \(\frac{1}{2}\) góc FOE)
Suy ra góc FIA=FKE, nhưng hai góc này lại ở vị trí SLT nên KE//AB
Đúng 0
Bình luận (1)
Cho 3 điểm A,B,C cố định, thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi nhưng luôn đi qua 2 điểm cố định C và B (O không thuộc BC). Từ A vẽ hai tiếp tuyến AM và AN với đường tròn (O) (M,N là 2 tiếp điểm ). Gọi I là trung điểm của BC.1, Chứng minh 4 điểm O,I,A,M cùng thuộc 1 đường tròn2, Gọi E,H lần lượt là giao điểm của OA cới đường tròn (O) và MN. Chứng minh BE là phân giác của góc ABH3,Chứng minh rằng tâm đường tròn ngoại tiếp tan giác OHI luôn nằm trên một đường thẳng cố định
Đọc tiếp
Cho 3 điểm A,B,C cố định, thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi nhưng luôn đi qua 2 điểm cố định C và B (O không thuộc BC). Từ A vẽ hai tiếp tuyến AM và AN với đường tròn (O) (M,N là 2 tiếp điểm ). Gọi I là trung điểm của BC.
1, Chứng minh 4 điểm O,I,A,M cùng thuộc 1 đường tròn
2, Gọi E,H lần lượt là giao điểm của OA cới đường tròn (O) và MN. Chứng minh BE là phân giác của góc ABH
3,Chứng minh rằng tâm đường tròn ngoại tiếp tan giác OHI luôn nằm trên một đường thẳng cố định
Cho ba điểm A, B, C cố định nằm trên một đường thẳng và theo thứ tự đó. Đường tròn (O) thay đổi luôn đi qua B và C. Từ A kẻ các tiếp tuyến AM và AN với đường tròn (O) (M, N là hai tiếp điểm). Đường thẳng MN cắt AO tại H, gọi E là trung điểm của BC. Chứng minh rằng khi đường tròn (O) thay đổi, tâm của đường tròn ngoại tiếp tam giác OHE nằm trên một đường tròn cố định
Đọc tiếp
Cho ba điểm A, B, C cố định nằm trên một đường thẳng và theo thứ tự đó. Đường tròn (O) thay đổi luôn đi qua B và C. Từ A kẻ các tiếp tuyến AM và AN với đường tròn (O) (M, N là hai tiếp điểm). Đường thẳng MN cắt AO tại H, gọi E là trung điểm của BC. Chứng minh rằng khi đường tròn (O) thay đổi, tâm của đường tròn ngoại tiếp tam giác OHE nằm trên một đường tròn cố định
Cho ba điểm A, B, C cố định nằm trên một đường thẳng và theo thứ tự đó. Đường tròn (O) thay đổi luôn đi qua B và C. Từ A kẻ các tiếp tuyến AM và AN với đường tròn (O) (M, N là hai tiếp điểm). Đường thẳng MN cắt AO tại H, gọi E là trung điểm của BC. Chứng minh rằng khi đường tròn (O) thay đổi, tâm của đường tròn ngoại tiếp tam giác OHE nằm trên một đường tròn cố định
Gọi I là giao điểm của MN và AC.
Ta có: \(\widehat{IHO}=\widehat{OEI}=90°\)
\(\Rightarrow\)Tứ giác EIHO nội tiếp đường tròn.
\(\Rightarrow\)Tâm của đường tròn ngoại tiếp ∆OHE nằm trên đường trung trực của EI.(*)
Ta có ∆AIH \(\approx\)∆AOE
\(\Rightarrow\)AH.AO = AE.AI (1)
Ta có: ∆AMB \(\approx\)AOM
\(\Rightarrow\)AM2 = AH.AO (2)
Ta lại có: ∆ABM \(\approx\)∆AMC
\(\Rightarrow\)AM2 = AB.AC (3)
Từ (1), (2), (3) \(\Rightarrow\)AE.AI = AB.AC
Vì A,B,C,E cố định nên I cố định (**)
Từ (*), (**) suy ta tâm đường tròn ngoại tiếp ∆OHE nằm trên đường trung trực của EI.
PS: không chứng minh được nó nằm trên đường tròn nha b. Hình tự vẽ.
Đúng 0
Bình luận (0)
bạn cho mình hỏi tại sao tam giác ABM đồng dạng với tam giác AMC vậy?. Mình ko hiểu chỗ đó
Đúng 0
Bình luận (0)
Ta có:
\(\widehat{BAM}=\widehat{MAC}\)(là góc chung)
\(\widehat{BMA}=\widehat{ACM}\) (Do AM là tiếp tuyến tại M của (O) và 2 góc đó cùng chắn cung MB)
\(\Rightarrow\Delta ABM\approx\Delta AMC\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
















