Trong mặt phẳng Oxy , có bao nhiêu đường thẳng d đi qua M(0;5) tạo với các trục tọa độ có diện tích bằng 5
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, đường thẳng đi qua điểm M(1;2) và vuông góc với đường thẳng d: 4x+2y+1=0 có phương trình tổng quát là
A. 4x-2y+3=0
B. 2x-4y+4=0
C. 2x-4y-6=0
D. x-2y+3=0
Trong mặt phẳng Oxy,đường thẳng d đi qua M(-2;3) và song song với đường thẳng EF.Biết E(0;-1),F(-3;0).Viết phương trình đường thẳng d
\(\overrightarrow{EF}=\left(-3;1\right)\)
Do d song song EF nên d nhận (1;3) là 1 vtpt
Phương trình d:
\(1\left(x+2\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-7=0\)
Đúng 1
Bình luận (1)
SGK Cánh Diều
13 tháng 8 2023 lúc 23:18
Trong mặt phẳng (P). Xét một điểm M tùy ý trong không gian.
a) Có bao nhiêu đường thẳng d đi qua điểm M và vuông góc với mặt phẳng (P)?
b) Đường thẳng d cắt mặt phẳng (P) tại bao nhiêu giao điểm?
a: Có 1 đường duy nhất
b: Đường thẳng d cắt (P) tại 1 giao điểm
Đúng 0
Bình luận (0)
trong mặt phẳng oxy, cho M(-1;1) , N(1;-3). Viết phương trình đường tròn đi qua hai điểm M,N và có tâm nằm trên đường thẳng d:2x-y+1=0
Gọi P là trung điểm MN \(\Rightarrow P\left(0;-1\right)\)
\(\overrightarrow{MN}=\left(2;-4\right)=2\left(1;-2\right)\Rightarrow\) trung trực của MN nhận (1;-2) là 1 vtpt
Phương trình trung trực MN:
\(1\left(x-0\right)-2\left(y+1\right)=0\Leftrightarrow x-2y-2=0\)
Gọi I là tâm đường tròn cần tìm \(\Rightarrow\) I là giao điểm của d và trung trực MN
Tọa độ I thỏa mãn: \(\left\{{}\begin{matrix}x-2y-2=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow I\left(-\dfrac{4}{3};-\dfrac{5}{3}\right)\)
\(\overrightarrow{IM}=\left(\dfrac{1}{3};\dfrac{8}{3}\right)\Rightarrow R^2=IM^2=\dfrac{65}{9}\)
Phương trình: \(\left(x+\dfrac{4}{3}\right)^2+\left(y+\dfrac{5}{3}\right)^2=\dfrac{65}{9}\)
Đúng 3
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, đường thẳng đi qua điểm
M
1
;
2
và vuông góc với đường thẳng
d
:
4
x
+
2
y
+
1
0
có phương trình tổng quát là A.
4
x
-
2
y
+
3
0
B.
2
x
-
4
y...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, đường thẳng đi qua điểm M 1 ; 2 và vuông góc với đường thẳng d : 4 x + 2 y + 1 = 0 có phương trình tổng quát là
A. 4 x - 2 y + 3 = 0
B. 2 x - 4 y + 4 = 0
C. 2 x - 4 y - 6 = 0
D. x - 2 y + 3 = 0
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d: \(mx+y+2=0\) và d': \(mx-4y+m+1=0\). Có bao nhiêu giá trị nguyên của m để d vuông góc d' ?
(d): VTPT là (m;1)
(d'): VTPT là (m;-4)
(d) vuông góc (d')
=>m^2-4=0
=>m=2 hoặc m=-2
=>Có 2 số nguyên m thỏa mãn
Đúng 0
Bình luận (0)
Giải mục 1 trang 78, 79, 80 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 21:50
Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d.a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d?b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?
Đọc tiếp
Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d.
a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d?
b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?
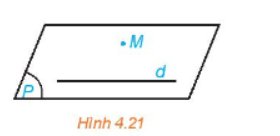
a) Có duy nhất một đường thẳng đi qua M song song với d
b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) vì hai đường thẳng song song đồng phẳng
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x-2y+1=0. Nếu đường thẳng ∆ qua điểm M (1;-1) và ∆ song song với d thì ∆ có phương trình là
A. x-2y+3=0
B. x-2y-3=0
C. x-2y+5=0
D. x+2y+1=0
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x-2y+10. Nếu đường thẳng ∆ qua điểm M (1;-1) và ∆ song song với d thì ∆ có phương trình là:
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x-2y+1=0. Nếu đường thẳng ∆ qua điểm M (1;-1) và ∆ song song với d thì ∆ có phương trình là:
Trong mặt phẳng tọa độ Oxy cho điểm M(1,-1)và hai đường thẳng có phương trình (d1):x - y - 1 = 0 và (d2) 2x+y-5=0. Gọi A là giao điểm của 2 đường thẳng trên . Biết rằng có 2 đường thẳng (d) đi qua M cắt 2 đường thẳng trên tại B,C sao cho tam giác ABC có BC=3AB .Tìm phương trình đường thẳng của 2 đường thẳng đó