Giải phương trình : x4 +2x3+5x2+4x-12=0
Mình đang rất gấp
Cảm ơn nhiều
Giải Phương trình
5x2 + 4x + 2x3 + x4 - 12 = 0
\(5x^2+4x+2x^3+x^4-12=0\)
\(\Leftrightarrow x^4+2x^3+5x^2+4x-12=0\)
\(\Leftrightarrow x^4-x^3+3x^3-3x^2+8x^2-8x+12x-12=0\)
\(\Leftrightarrow x^3\left(x-1\right)+3x^2\left(x-1\right)+8x\left(x-1\right)+12\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^3+3x^2+8x+12\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^3+2x^2+x^2+2x+6x+12\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^2\left(x+2\right)+x\left(x+2\right)+6\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2+x+6\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[x^2+2\times\dfrac{1}{2}x+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{1}{2}\right)^2+6\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+\dfrac{1}{2}\right)^2+\dfrac{23}{4}\right]\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x+2=0\\\left(x^2+\dfrac{1}{2}\right)^2+\dfrac{23}{4}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Vì \(\left(x^2+\dfrac{1}{2}\right)^2\ge0\forall x\Rightarrow\left(x^2+\dfrac{1}{2}\right)^2+\dfrac{23}{4}\ge\dfrac{23}{4}\forall x\)
\(\Rightarrow\left(x^2+\dfrac{1}{2}\right)^2+\dfrac{23}{4}\) vô nghiệm
Vậy phương trình có tập nghiệm là\(S=\left\{1;-2\right\}\)
Cho phương trình 4x^2 + 4(2m+3)x +4m^2 - 3= 0 có 2 nghiêm x1, x2 thỏa x1^2 +x2^2 =1/2
Bạn nào giải giúp mik với ạ
mình đang cần gấp
Cảm ơn <3
PT có 2 nghiệm `<=> \Delta' >=0`
`<=> 4(2m+3)^2 -4(4m^2-3) >=0`
`<=>16m^2+48m+36-16m^2+12>=0`
`<=>m >= -1`
Viet: `{(x_1+x_2=-2m-3),(x_1x_2=4m^2-3):}`
Theo đề: `x_1^2+x_2^2=1/2`
`<=>(x_1+x_2)^2-2x_1x_2=1/2`
`<=>(-2m-3)^2 -2(4m^2-3)=1/2`
`<=>-4m^2+12m+15=1/2`
`<=>` \(\left[{}\begin{matrix}m=\dfrac{6+\sqrt{94}}{4}\left(TM\right)\\m=\dfrac{6-\sqrt{94}}{4}\left(L\right)\end{matrix}\right.\)
Vậy....
F(x)=x4+5x2-4x+x5-x4-8x2+3+2x3+2
Thu gọn và sắp xếp phải k ạ?
`F(x)= (x^4-x^4)+(5x^2-8x^2)-4x+x^5+3+2x^3+2`
`F(x) = -3x^2-4x+x^5+3+2x^3+2`
`F(x)= x^5+2x^3-3x^2-4x+3+2`
\(F\left(x\right)=x^4+5x^2-4x+x^5-x^4-8x^2+3+2x^3+2\)
\(F\left(x\right)=x^5+\left(x^4-x^4\right)+2x^3+\left(5x^2-8x^2\right)-4x+\left(3+2\right)\)
\(F\left(x\right)=x^5+2x^3-3x^2-4x+5\)
Giải phương trình sau bằng cách đưa về phương trình tích: 2x3 + 5x2 – 3x = 0
2x3 + 5x2 – 3x = 0
⇔ x(2x2 + 5x – 3) = 0
⇔ x.(2x2 + 6x – x – 3) = 0
⇔ x. [2x(x + 3) – (x + 3)] = 0
⇔ x.(2x – 1)(x + 3) = 0
⇔ x = 0 hoặc 2x – 1 = 0 hoặc x + 3 = 0
+ 2x – 1 = 0 ⇔ 2x = 1 ⇔ x = 1/2.
+ x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm 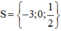
Phân tích
a,(x2 + x + 2)3 - (x+1)3 = x6 +1 b,(x2 + 10x + 8)2 - (8x + 4)(x2 + 8x+7)
c, A= x4 + 2x3 + 3x2 + 2x+4 d,B= x4 + 4x3 + +8x2 + 8x + 4
e, C= x4 - 2x3 + 5x2 - 4x + 4
Phân tích đa thức thành nhân tử bằng phương pháp đặt ẩn phụ
x4+2x3+5x2+4x-12
`x^4+2x^3+5x^2+4x-12`
`=x^4-x^3+3x^3-3x^2+8x^2-8x+12x-12`
`=x^3(x-1)+3x^2(x-1)+8x(x-1)+12(x-1)`
`=(x-1)(x^3+3x^2+8x+12)`
`=(x-1)(x^3+2x^2+2x^2+4x+6x+12)`
`=(x-1)[x^2(x+2)+2x(x+2)+6(x+2)]`
`=(x-1)(x+2)(x^2+2x+6)`
\(x^4+2x^3+5x^2+4x-12\)
\(=x^4-x^3+3x^3-3x^2+8x^2-8x+12x-12\)
\(=\left(x-1\right)\left(x^3+3x^2+8x+12\right)\)
\(=\left(x-1\right)\left(x^2+2x^2+x^2+2x+6x+12\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+6\right)\)
Giải các phương trình trùng phương: x4 – 5x2 + 4 = 0
x4 – 5x2 + 4 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t2 – 5t + 4 = 0 (2)
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t1 = 1; t2 = c/a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
Giải các phương trình: x4 + 5x2 + 1 = 0
x4 + 5x2 + 1 = 0 (1)
Đặt x2 = t, t > 0.
(1) trở thành: t2 + 5t + 1 = 0 (2)
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 52 – 4.1.1 = 21 > 0
⇒ Phương trình có hai nghiệm:
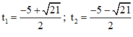
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Giải phương trình:
a) x4 - 2x3 + x2 - 4x +4 = 0
b) x4 + 2x3 - 3 = 0
c) 2x4 - 100x + 98 = 0
d) (x + 1)(x + 2)(x + 3)(x + 4) = 24
d: Ta có: \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)=24\)
\(\Leftrightarrow\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24=0\)
\(\Leftrightarrow x\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)