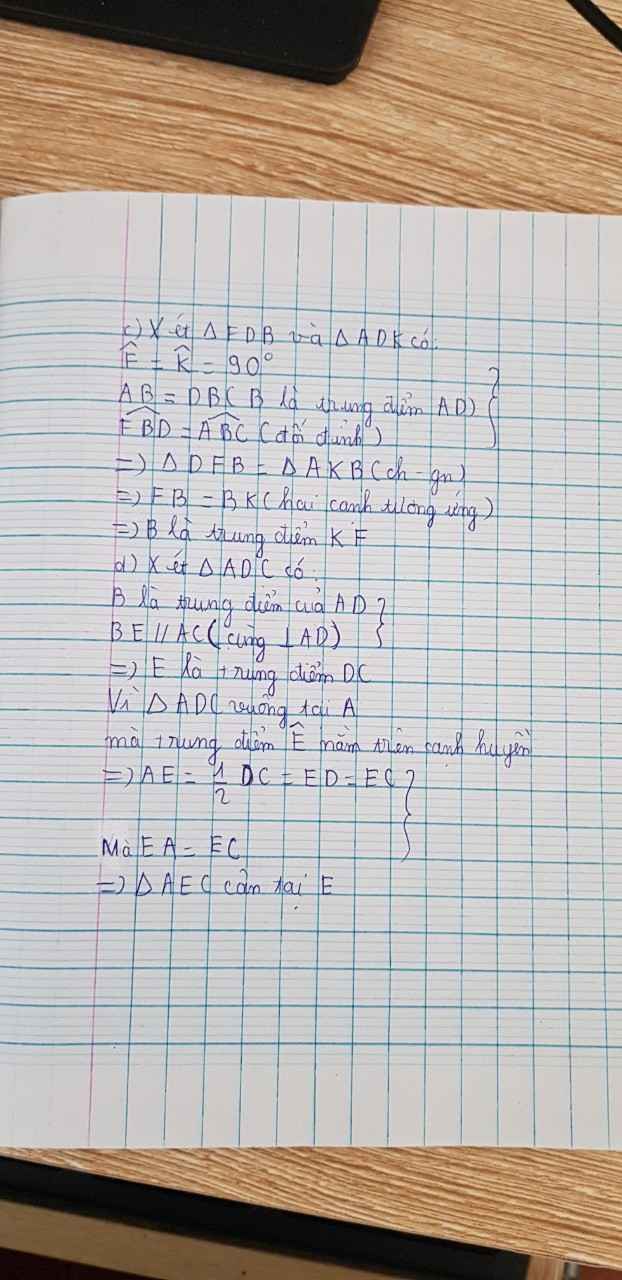Cho tam giác ABC vuông tại A có AB=5cm, AC=12cm
a) Tính BC.
b) Kéo dài AB lấy D sao cho B là trung điểm của AD. Nối CD, qua B vẽ đường thẳng vuông góc với AD cắt CD tại E. Chứng minh tam giác ABE=tam giác DBE và suy ra tam giác AED cân.
c) Kẻ AK vuông góc với BC tại K. Qua D kẻ đường thẳng vuông góc với đường thẳng BC tại F. Chứng minh B là trung điểm của KF.
d) Chứng minh tam giác AEC cân và suy ra E là trung điểm của DC.
Các bạn giúp mình nhé =)))
Mai mình pải nộp cho cô rồi =((((
Không cần vẽ hình đâu cbạn =))))
#helpmeplz